Petite question sur les EV / SEV

[Ihaveadream]

Bonjour à tous,
Je me pose une question : Est ce la même chose lorsque l'on nous demande démontrer qu'un ensemble est un un sous espace vectoriel et lorsque l'on demande simplement que c'est un espace vectoriel ?
Enfin je veux dire, je sais que ce n'est pas pareil mais est-ce toujours la même démarche ? Ensemble non vide + montrer que pour lambda et nu scalaires et u et v appartenant a l’ensemble , lambda*u+nu*v appartient toujours à l’ensemble ?
Merci par avance

[Archytas]

Bonjour à tous,
Je me pose une question : Est ce la même chose lorsque l'on nous demande démontrer qu'un ensemble est un un sous espace vectoriel et lorsque l'on demande simplement que c'est un espace vectoriel ?
Enfin je veux dire, je sais que ce n'est pas pareil mais est-ce toujours la même démarche ? Ensemble non vide + montrer que pour lambda et nu scalaires et u et v appartenant a l’ensemble , lambda*u+nu*v appartient toujours à l’ensemble ?
Merci par avance

Salut, ça dépend des contextes, si tu sais que ton ensemble est inclu dans un espace vectoriel alors c'est la démarche la plus intelligente en effet mais si tu n'as pas d'espaces vectoriels dans lequel est inclu ton ensemble (ou tu n'en connais pas), il faut revenir à la définition et tout redémontrer (et oui...).

[Archibald]

Bonjour,

oui souvent la même démarche : ensemble non vide, stable par addition (loi de composition interne) + stable par homothétie (loi de composition externe) = stable par combinaison linéaire.


Garde en tête qu'un sous-espace vectoriel est lui-même un espace vectoriel mais d'une dimension inférieure à l'espace vectoriel dans lequel il est contenu.

[Archytas]

Garde en tête qu'un sous-espace vectoriel est lui-même un espace vectoriel mais d'une dimension inférieure à l'espace vectoriel dans lequel il est contenu.

Oui c'est ça, quand on peut parler de dimension bien sûr !

[Ihaveadream]

Merci, c'est vrai que c'est logique, un sous espace vectoriel est forcément un espace vectoriel mais pas l'inverse.

Merci à vous deux pour vos réponses :) !

[Ihaveadream]

Par contre il y a autre chose que je ne comprends pas, comment prouver qu'une matrice est un SEV, j'arrive à prouver que l'ensemble n'est pas vide mais pas à prouver que la somme reste dans l’ensemble
Par exemple pour la matrice M2
a+b b
b a

elle est équivalente à :
a [HTML]1 0
0 1[/HTML] + b [html]1 1
1 0[/html]

Mais ensuite je ne sais pas comment procéder ... :s

[Archytas]

Attention au vocabulaire, une matrice n'est jamais un espace vectoriel. C'est l'ensemble des matrices constitué des matrices de la formes que tu viens de décrire. Tu prend une matrice avec a et b et une avec c et d, tu les sommes et tu montres que la somme est toujours de la même forme que tu viens de décrire précedément !

[Archibald]

Prends une nouvelle matrice et prouve que est de la forme
en donnant , , en fonction des autres coefficients.

Edit : Archytas, encore une fois plus rapide.

[Archytas]

Edit : Archytas, encore une fois plus rapide.

Tant mieux, ça fait deux versions, c'est toujours mieux (; ! Et j'ai eu clairement la flemme d'expliquer, c'est plus facile à comprendre comme tu l'as dis ! D'ailleurs pour faire d'une pierre deux coups on peux calculer directement M(a,b)+k*M(a',b') !

[mrif]

Par contre il y a autre chose que je ne comprends pas, comment prouver qu'une matrice est un SEV, j'arrive à prouver que l'ensemble n'est pas vide mais pas à prouver que la somme reste dans l’ensemble
Par exemple pour la matrice M2
a+b b
b a

elle est équivalente à :
a [HTML]1 0
0 1[/HTML] + b [html]1 1
1 0[/html]

Mais ensuite je ne sais pas comment procéder ... :s

Le gros du travail est fait: tu as montré que ton esapce M2 est l'espace engendré par les 2 matrices donc c'est un sous espace vectoriel. Les 2 matrices sont linéairement indépendantes et du coup tu as même la dimension du sous espace vectoriel.

[Ihaveadream]

@Archibald et @archytas donc c'est bon si je fait comme ça :

?

(je n'ai pas reussi a passé a la ligne dans la matrice, les slashs représentent un changement de ligne..

@mrif Donc un espace engendré par les 2 matrices est forcement un sous espace vectoriel ? pourquoi ça ? je ne vois pas vraiment le lien avec les conditions d'un sev :/ ...

[Archibald]

Je voulais t'en parler à mon premier poste mais je ne voulais pas t'embrouiller. Regarde cet exemple classique :



C'est pareil avec les matrices, quoique légèrement plus abstrait.

[mrif]

@Archibald et @archytas donc c'est bon si je fait comme ça :

?

(je n'ai pas reussi a passé a la ligne dans la matrice, les slashs représentent un changement de ligne..

@mrif Donc un espace engendré par les 2 matrices est forcement un sous espace vectoriel ? pourquoi ça ? je ne vois pas vraiment le lien avec les conditions d'un sev :/ ...

C'est du cours: tout sous ensemble d'un espace vectoriel engendré par une famille de vecteurs est un sous espace vectoriel.
M2 = {aI + bJ | a et b dans R} si on appelle I et J les 2 matrices génératrices.
D'autre part il n'existe pas de scalaire t tq J = tI donc cette famille est libre et on déduit dim(M2) = 2.

Il n'est pas nécessaire de retourner toujours aux définitions pour répondre aux questions. Il est plus judicieux d'utiliser les outils du cours qui aboutissent le plus facilement aux résultats demandés.

[Archibald]

Un schéma qui peut t'aider :

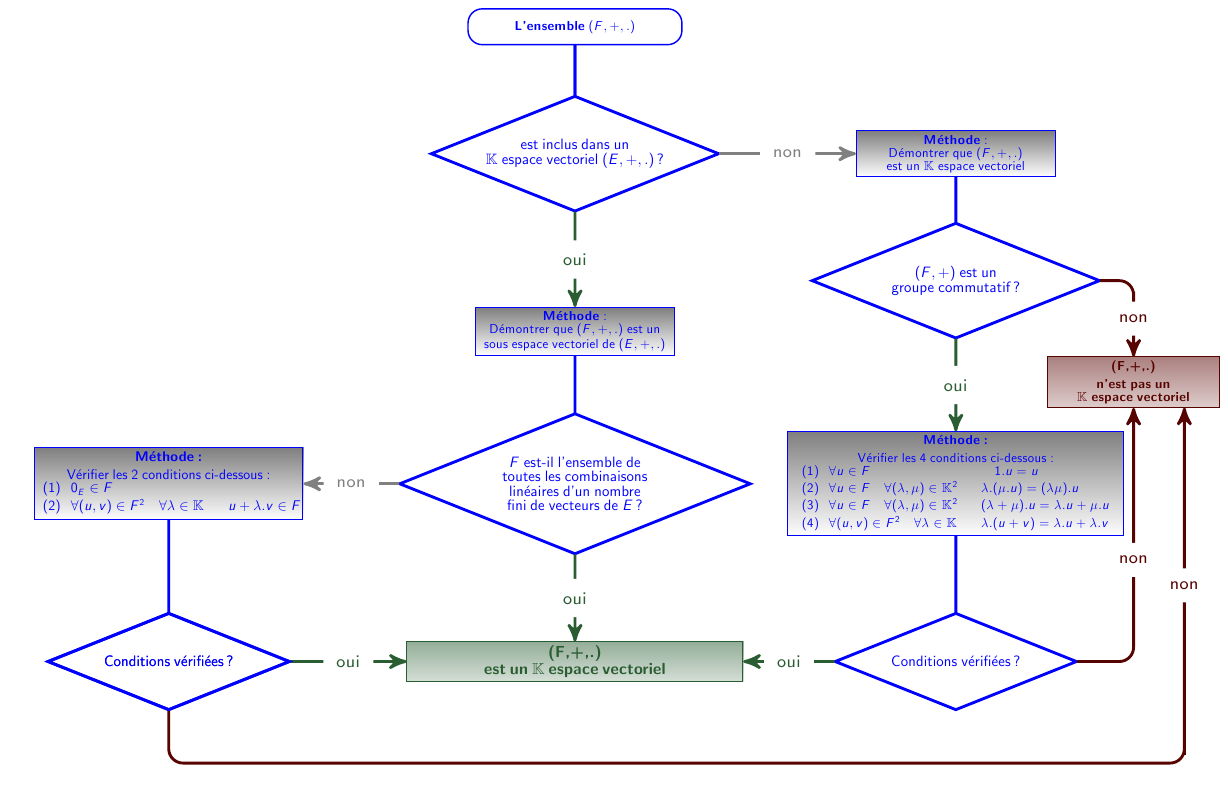
[Ihaveadream]

Merci à tous !!
Et merci pour le schéma Archibald