[DM] La racine carrée de 2 !
19 messages
- Page 1 sur 1
[DM] La racine carrée de 2 !
[FONT=Tahoma]B[/FONT]onjour à toutes et à tous,
[FONT=Trebuchet MS]Actuellement en classe de troisième, j'ai un devoir maison à rendre d'ici la fin des vacances et il s'avère que j'ai quelques difficultés à faire ce DM.
J'ai commencé à réfléchir pour certaines questions mais sans succès...
Assez de blabla, je vous expose l'énoncé ainsi que les recherches que j'ai déjà faites :
[/FONT]
3 - Irrationalité de la racine carrée de 2
Toutes ces tentatives firent vaines, car il est aujourd'hui démontré que ce nombre r, dont le carré est égal à 2, ne peut pas être écrit sous la forme d'un nombre rationnel : On dit qu'il est irrationnel !!. C'est ce résultat que Pythagore voulut cacher à tout prix, pour ne pas voir son système philosophique mis à mal : la légende raconte même qu'un des disciples de Pythagore, nommé Hippase de Métaponte, fut noyé par ses codisciples pour avoir révélé ce secret au grand public !
En voici la démonstration ( basée sur la démonstration par l'absurde ) :
Suppossons que r est un rationnel, et donc que l'on peut écrire r sous la forme d'un quotient : r = a/b,
avec a et b entiers naturels non nuls premiers entre eux (la fraction a/b est dont supposée irréductible).
1. Montrer que a² = 2b² ; en déduire que a² est pair.
Mes recherches :
On sait que r² = 2 soit :
r = a/b
INDICE :-Produit en croix-
---------------------------
2. Completer le tableau suivant :
Le nombre a se termine par .. 0 | 1 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Le nombre a² se termine par ..
Je l'ai rempli sans difficulté.
---------------------------
3. Déduire des questions précedentes que a est nécessairement un nombre pair.
---------------------------
4. Posons donc a = 2p avec p entier naturel. Déduire de la question 1 que b² est nécessairement un nombre pair, et donc que le b l'est aussi.
---------------------------
5. En quoi ce dernier résultat est-il contradictoire avec notre supposition de départ? Conclure ...
---------------------------
[FONT=Tahoma]J[/FONT]e vous remercie d'avance !
[FONT=Trebuchet MS]Actuellement en classe de troisième, j'ai un devoir maison à rendre d'ici la fin des vacances et il s'avère que j'ai quelques difficultés à faire ce DM.
J'ai commencé à réfléchir pour certaines questions mais sans succès...
Assez de blabla, je vous expose l'énoncé ainsi que les recherches que j'ai déjà faites :
[/FONT]
3 - Irrationalité de la racine carrée de 2
Toutes ces tentatives firent vaines, car il est aujourd'hui démontré que ce nombre r, dont le carré est égal à 2, ne peut pas être écrit sous la forme d'un nombre rationnel : On dit qu'il est irrationnel !!. C'est ce résultat que Pythagore voulut cacher à tout prix, pour ne pas voir son système philosophique mis à mal : la légende raconte même qu'un des disciples de Pythagore, nommé Hippase de Métaponte, fut noyé par ses codisciples pour avoir révélé ce secret au grand public !
En voici la démonstration ( basée sur la démonstration par l'absurde ) :
Suppossons que r est un rationnel, et donc que l'on peut écrire r sous la forme d'un quotient : r = a/b,
avec a et b entiers naturels non nuls premiers entre eux (la fraction a/b est dont supposée irréductible).
1. Montrer que a² = 2b² ; en déduire que a² est pair.
Mes recherches :
On sait que r² = 2 soit :
r = a/b
INDICE :-Produit en croix-
---------------------------
2. Completer le tableau suivant :
Le nombre a se termine par .. 0 | 1 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Le nombre a² se termine par ..
Je l'ai rempli sans difficulté.
---------------------------
3. Déduire des questions précedentes que a est nécessairement un nombre pair.
---------------------------
4. Posons donc a = 2p avec p entier naturel. Déduire de la question 1 que b² est nécessairement un nombre pair, et donc que le b l'est aussi.
---------------------------
5. En quoi ce dernier résultat est-il contradictoire avec notre supposition de départ? Conclure ...
---------------------------
[FONT=Tahoma]J[/FONT]e vous remercie d'avance !
Pour la deuxième partie de ta question 1, faut chercher bien loin : comme  , cela équivaut directement à dire que
, cela équivaut directement à dire que  est un multiple de 2, et qu'il est donc divisible par ce nombre. Tu peux aussi dire que
est un multiple de 2, et qu'il est donc divisible par ce nombre. Tu peux aussi dire que  équivaut à
équivaut à  , or
, or  étant un entier,
étant un entier,  aussi et donc
aussi et donc  est divisible par deux.
est divisible par deux.
Pour la 3, tu peux le démontrer en partant des définitions des nombres pairs et impairs. Un nombre pair peut s'écrire sous la forme
peut s'écrire sous la forme  ,
,  étant un nombre entier; un nombre impair
étant un nombre entier; un nombre impair  s'écrit en revanche sous la forme
s'écrit en revanche sous la forme  .
.
Un nombre entier forcément soit pair, soit impair, en calculant les carrés de ces deux cas de figure tu devrais te rendre compte de quelque chose.
Pour la 3, tu peux le démontrer en partant des définitions des nombres pairs et impairs. Un nombre pair
Un nombre entier forcément soit pair, soit impair, en calculant les carrés de ces deux cas de figure tu devrais te rendre compte de quelque chose.
Merci,
Ensuite pour la question 3 :
3. Déduire des questions précédentes que a est nécessairement pair.
J'ai remarqué un truc, c'est que lorsque l'on multiplie par 2 le carrée d'un entier naturels (qu'il soit pair ou impair ) , on obtient toujours un chiffre pair
d'ou : a² = 2b²
et que a² est pair
J'avais vu quelques part que le carré d'un entier naturel est pair et inversement. Je me trompe peut être.
Mais il faut maintenant le démontrer et c'est la que je bloque...
Ensuite pour la question 3 :
3. Déduire des questions précédentes que a est nécessairement pair.
J'ai remarqué un truc, c'est que lorsque l'on multiplie par 2 le carrée d'un entier naturels (qu'il soit pair ou impair ) , on obtient toujours un chiffre pair
d'ou : a² = 2b²
et que a² est pair
J'avais vu quelques part que le carré d'un entier naturel est pair et inversement. Je me trompe peut être.
Mais il faut maintenant le démontrer et c'est la que je bloque...
WaylZHP a écrit:Merci,
Ensuite pour la question 3 :
3. Déduire des questions précédentes que a est nécessairement pair.
J'ai remarqué un truc, c'est que lorsque l'on multiplie par 2 le carrée d'un entier naturels (qu'il soit pair ou impair ) , on obtient toujours un chiffre pair
d'ou : a² = 2b²
et que a² est pair
J'avais vu quelques part que le carré d'un entier naturel est pair et inversement. Je me trompe peut être.
Mais il faut maintenant le démontrer et c'est la que je bloque...
Là tu étais bien parti ...a² est pair, un nombre est pair lorsqu'il est divisible par 2 et tu as du apprendre qu'un nombre est divisible par 2 si il se termine par 0,2,4,6 ou 8 ... regarde dans le tableau quand est-ce que a² est un nombre pair et par quoi se termine a dans ces cas là ?
triumph59 a écrit:Regarde par quel chiffre se termine a lorsqueest pair
exemple : sise termine par 0, a se termine par 0
... je te laisse continuer
Dans ce cas, si
si
si
si
si
WaylZHP a écrit:Dans ce cas, siest pair,
se termine soit par 0, 4, 16, 36, 64 etc.
sise termine par 4, a se termine par 2
sise termine par 16, a se termine par 4
sise termine par 36, a se termine par 6
sise termine par 64, a se termine par 8
Tu peux simplifier encore en disant
si
si
si
si
si
Conclusion,
C'est vrai que c'est tout de suite plus simple.
Ainsi je peux m'attaquer à la question 4 :
Ca donne :
Si je part de la question 1 :

)





Sachant que p est un entier naturel (= a ) et que , On peut dire que
, On peut dire que 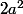 et
et  est un multiple de 2 et donc divisible par 2 car
est un multiple de 2 et donc divisible par 2 car  soit l'équivalent de
soit l'équivalent de 
 est donc pair et que
est donc pair et que  l'est aussi si et seulement si :
l'est aussi si et seulement si :
 se termine par 0 alors
se termine par 0 alors  se termine par 0
se termine par 0
 se termine par 4, alors
se termine par 4, alors  se termine par 0
se termine par 0
 se termine par 6, alors
se termine par 6, alors  se termine par 0
se termine par 0
 se termine par 6, alors
se termine par 6, alors  se termine par 0
se termine par 0
 se termine par 4, alors
se termine par 4, alors  se termine par 8
se termine par 8
On en conclue que est pair lorsque
est pair lorsque  l'est aussi.
l'est aussi.
Ce qui mène à la question 5 ensuite .. car on a vu que alors que à la question 4, on a démontrer que
alors que à la question 4, on a démontrer que  .
.
Ainsi je peux m'attaquer à la question 4 :
Posons donc a = 2p avec p entier naturel. Déduire de la question 1 que b² est nécessairement un nombre pair, et donc que le b l'est aussi.
Ca donne :
Si je part de la question 1 :
Sachant que p est un entier naturel (= a ) et que
On en conclue que
Ce qui mène à la question 5 ensuite .. car on a vu que
WaylZHP a écrit:C'est vrai que c'est tout de suite plus simple.
Ainsi je peux m'attaquer à la question 4 :
Ca donne :
Si je part de la question 1 :
Sachant que p est un entier naturel (= a ) et que, On peut dire que
et
est un multiple de 2 et donc divisible par 2 car
soit l'équivalent de
est donc pair et que
l'est aussi si et seulement si :
se termine par 0 alors
se termine par 0
se termine par 4, alors
se termine par 0
se termine par 6, alors
se termine par 0
se termine par 6, alors
se termine par 0
se termine par 4, alors
se termine par 8
On en conclue queest pair lorsque
l'est aussi.
Ce qui mène à la question 5 ensuite .. car on a vu quealors que à la question 4, on a démontrer que
.
Une fois de plus, tu te compliques la vie ... tu sais que a²=2b² et à présent tu sais que a s'écrit sous la forme a=2p car a est un nombre pair
Il te suffit de remplacer a par 2p et l'égalité devient (2p)²=2b2 fait simplement le calcul 4p²=2b², en simplifiant 2p²=b² ou encore b²=2p² et tu retrouves une égalité similaire à celle de départ avec a²=2b² ... et sans refaire la demonstration (elle serait exactement la même) b est pair
J'attends ta conclusion pour le 5)
Oui, j'ai tendance à chercher le petit bout x)
D'après la question, On sait que vaut
vaut 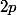 ce qui donne :
ce qui donne :
 (J'ai pas compris pourquoi tu as placé des parenthèse mais on arrive au final au même raisonnement ) qui pourrai se simplifier en
(J'ai pas compris pourquoi tu as placé des parenthèse mais on arrive au final au même raisonnement ) qui pourrai se simplifier en  ou encore
ou encore  qui ressemble à l'égalité de départ
qui ressemble à l'égalité de départ 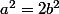
 est alors pair ainsi que
est alors pair ainsi que  si et seulement si :
si et seulement si :
 se termine par 0 alors
se termine par 0 alors  se termine par 0
se termine par 0
 se termine par 4, alors
se termine par 4, alors  se termine par 0
se termine par 0
 se termine par 6, alors
se termine par 6, alors  se termine par 0
se termine par 0
 se termine par 6, alors
se termine par 6, alors  se termine par 0
se termine par 0
 se termine par 4, alors
se termine par 4, alors  se termine par 8.
se termine par 8.
--------------
Ensuite pour la dernière question :
Selon la supposition de départ, peut s'écrire sous forme d'un quotient : a/b sachant que
peut s'écrire sous forme d'un quotient : a/b sachant que  et
et  sont des entiers naturels non nuls premiers entre eux .
sont des entiers naturels non nuls premiers entre eux .
On a vu que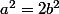 et que
et que  est pair ainsi que son carré de même pour
est pair ainsi que son carré de même pour  .
.
Or d'après la supposition de départ, et
et  sont premiers entre eux, ce qui est contradictoire avec ce qu'on a démontré avec
sont premiers entre eux, ce qui est contradictoire avec ce qu'on a démontré avec et
et  qui sont tous les deux pairs.
qui sont tous les deux pairs.
Ajoutons aussi que cette égalité ne peut avoir lieu que si a est pair car si est impair son carré l'est aussi et ne peut être égal à
est impair son carré l'est aussi et ne peut être égal à  qui est pair.
qui est pair.
On en conclue que ne peut être écrit sous forme d'une fraction rationnelle irréductible.
ne peut être écrit sous forme d'une fraction rationnelle irréductible.
D'après la question, On sait que
--------------
Ensuite pour la dernière question :
Selon la supposition de départ,
On a vu que
Or d'après la supposition de départ,
Ajoutons aussi que cette égalité ne peut avoir lieu que si a est pair car si
On en conclue que
WaylZHP a écrit:Oui, j'ai tendance à chercher le petit bout x)
D'après la question, On sait quevaut
ce qui donne :
(J'ai pas compris pourquoi tu as placé des parenthèse mais on arrive au final au même raisonnement ) qui pourrai se simplifier en
ou encore
qui ressemble à l'égalité de départ
est alors pair ainsi que
si et seulement si :
se termine par 0 alors
se termine par 0
se termine par 4, alors
se termine par 0
se termine par 6, alors
se termine par 0
se termine par 6, alors
se termine par 0
se termine par 4, alors
se termine par 8.
--------------
Ensuite pour la dernière question :
Selon la supposition de départ,peut s'écrire sous forme d'un quotient : a/b sachant que
et
sont des entiers naturels non nuls premiers entre eux .
On a vu queet que
est pair ainsi que son carré de même pour
.
Or d'après la supposition de départ,et
sont premiers entre eux, ce qui est contradictoire avec ce qu'on a démontré avec
et
qui sont tous les deux pairs.
Ajoutons aussi que cette égalité ne peut avoir lieu que si a est pair car siest impair son carré l'est aussi et ne peut être égal à
qui est pair.
On en conclue quene peut être écrit sous forme d'une fraction rationnelle irréductible.
J'ai précisé les parenthèses pour distinguer (2p)² et 2p2 !! au final si a et b sont pairs il serait possible de simplifier la fraction a/b en divisant a et b par 2 ... on a supposé que a/b était une fraction irreductible ... c'est donc contradictoire CQFD
19 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 21 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
