Dérivées
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
zlatan01
- Membre Naturel
- Messages: 18
- Enregistré le: 23 Jan 2013, 09:01
-
 par zlatan01 » 24 Jan 2013, 09:13
par zlatan01 » 24 Jan 2013, 09:13

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 24 Jan 2013, 09:35
par chan79 » 24 Jan 2013, 09:35
zlatan01 a écrit:bonjour, j'aimerai savoir si j'ai bien dérivée et si j'ai assez simplifier!
1)
=\frac{\sqrt{x}-1}{x-1})
attention aux parenthèses
=\frac{{\frac{x-1}{2\sqrt{x}}-(\sqrt{x}-1)}}{(x-1)^2})
tu as aussi
=\frac{\sqrt{x}-1}{x-1}=\fra{1}{\sqr{x}+1})
avec x différent de 1
ce qui permet d'avoir une autre forme plus intéressante de f'(x)
pour le 2
erreur pour v'(x)

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 24 Jan 2013, 09:43
par ampholyte » 24 Jan 2013, 09:43
Bonjour,
1)
Attention aux parenthèses !
=\frac{{\frac{x-1}{2\sqrt{x}}-(\sqrt{x}-1)}}{(x-1)^2}.)
Tu peux mettre le numérateur au même denominateur pour te ramener à une fonction
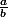
. N'oublie pas que
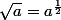
et que

2) Attention ici
=(\sqrt{x}+1)^3)
alors
 = 3 * (\sqrt{x} + 1)' * (\sqrt{x} + 1)^2)
Si on a la fonction
 = u(x)^n)
alors
 = n u'(x) * u(x) ^ {n - 1})
Je te laisse reprendre ton calcul.
3) Attention aux parenthèses
' = \frac{(u')*(v) - (u)(v')}{v^2})
4) Idem que 2.
 = \sqrt{u(x)} = u(x)^{\frac{1}{2}})
 = \frac{1}{2} * u'(x) * u(x)^{\frac{-1}{2}} = {\frac{u'(x)}{2u(x)}})
5) J'ai pas compris ton calcul pour la 5, que dois-tu faire ?
Je te laisse reprendre ton calcul.
-
zlatan01
- Membre Naturel
- Messages: 18
- Enregistré le: 23 Jan 2013, 09:01
-
 par zlatan01 » 24 Jan 2013, 10:39
par zlatan01 » 24 Jan 2013, 10:39
pour la 5) il faut aussi dériver mais j'ai déjà simplifier et j'ai obtenu 0 je sais si j'ai bien fait..?!? et je refait les autres avec vos réponses et je remet mes réponses merci déjà

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 24 Jan 2013, 10:42
par ampholyte » 24 Jan 2013, 10:42
=\sqrt{\frac{x^2 -x+2}{x(x+1)}})
Je ne vois pas comment tu obtiens 0.
Tu dois procéder de la même manière qu'avant :
 = \frac{1}{2} * u'(x) * u(x)^{\frac{-1}{2}} = {\frac{u'(x)}{2u(x)}})
Avec
 = \frac{x^2 -x+2}{x(x+1)})
donc u(x) est de la forme
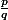
donc
 =\frac{p'q - q'p}{q^2})
-
zlatan01
- Membre Naturel
- Messages: 18
- Enregistré le: 23 Jan 2013, 09:01
-
 par zlatan01 » 24 Jan 2013, 10:54
par zlatan01 » 24 Jan 2013, 10:54
j'ai développé x(x+1) et du coup sa supprime le x² et le x en haut et en bas et sa donne en simplifiant

et donc sa fait zéro (et je disais bien que j'avais faux sa aurai été trop facile sinon..!
Bon je vous donne mes réponses demain au plus tard merci.

-
ampholyte
- Membre Transcendant
- Messages: 3940
- Enregistré le: 21 Juil 2012, 07:03
-
 par ampholyte » 24 Jan 2013, 11:00
par ampholyte » 24 Jan 2013, 11:00
Euh, attention
} = \frac{x^2 - x + 2}{x^2 + x})
Je ne vois vraiment pas comment tu peux simplifier cela.
Revois ton cours sur les fractions car les simplifications de fraction est vu au collège normalement. Cela revient au même pour des fractions de polynômes.

et non 0.

ne se simplifie pas !!
De plus

, une division par 0 est interdite, et ne fait en aucun 0.
-
zlatan01
- Membre Naturel
- Messages: 18
- Enregistré le: 23 Jan 2013, 09:01
-
 par zlatan01 » 24 Jan 2013, 11:02
par zlatan01 » 24 Jan 2013, 11:02
c'est bien ce qu'il me semblais mais bon j'ai du mal a reprendre les cours :S faut que je reprenne les bases en mains et sa ira mieux dans quelles que mois :)
-
zlatan01
- Membre Naturel
- Messages: 18
- Enregistré le: 23 Jan 2013, 09:01
-
 par zlatan01 » 28 Jan 2013, 09:29
par zlatan01 » 28 Jan 2013, 09:29
pour le 1) j'ai trouver
= \frac{\frac{-1}{2} x^-0.5}{(\sqrt{x} +1)^2})
pour le 2) =>
=3(\sqrt{x} +1)(\sqrt{x} +1)^2)
Donc
=(\sqrt{x} +1)^3 +x[3(\sqrt{x} +1)(\sqrt{x} +1)^2])
J'arrive pas a plus simplifier..
pour le 3) j'ai pas trouver mon erreur
le 4) j'ai pas comprit votre formule..
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 178 invités