Série entière
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Ellhaym
- Membre Naturel
- Messages: 47
- Enregistré le: 17 Aoû 2010, 22:18
-
 par Ellhaym » 22 Jan 2013, 22:48
par Ellhaym » 22 Jan 2013, 22:48
Bonsoir à vous
Soit

Une Série entière
On a

= n! et an = 0 si n =/=
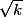
avec k dans IN
Comment je détermine le rayon de convergence ? :we: , comment appliquer la règle de d'alembert?
Merci à vous
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 22 Jan 2013, 22:55
par girdav » 22 Jan 2013, 22:55
C'est lacunaire, on ne peut pas appliquer d'Alembert.
Par contre, on peut essayer de revenir à la définition du rayon de convergence : quel est l'ensemble des

tels que la suite
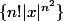
soit bornée ?
-
Ellhaym
- Membre Naturel
- Messages: 47
- Enregistré le: 17 Aoû 2010, 22:18
-
 par Ellhaym » 22 Jan 2013, 23:30
par Ellhaym » 22 Jan 2013, 23:30
girdav a écrit:C'est lacunaire, on ne peut pas appliquer d'Alembert.
Par contre, on peut essayer de revenir à la définition du rayon de convergence : quel est l'ensemble des

tels que la suite
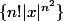
soit bornée ?
La suite
\mid^(n^2))
est bornée pour x compris entre -1 et 1 je suppose, la factorielle me pose problème
Pourquoi ne pourrait on pas prendre la borne sup de (

) pour un indice n n'étant pas un carré et on tirer les conclusions?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 23 Jan 2013, 11:31
par girdav » 23 Jan 2013, 11:31
C'est le

qui fait que le rayon de convergence est nul.
-
MMu
- Membre Relatif
- Messages: 399
- Enregistré le: 11 Déc 2011, 22:43
-
 par MMu » 23 Jan 2013, 16:14
par MMu » 23 Jan 2013, 16:14
girdav a écrit:C'est le

qui fait que le rayon de convergence est nul.
Pas d'accord , le rayon de convergence est

.
Pour

On a alors
|x|^{n^2}=(n!)(|x|^n)^n<)
^n)
ce qui assure la convergence .
Do you follow me ? ... :zen:
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 23 Jan 2013, 16:34
par girdav » 23 Jan 2013, 16:34
MMu a écrit:Pas d'accord , le rayon de convergence est

.
Pour

On a alors
|x|^{n^2}=(n!)(|x|^n)^n<)
^n)
ce qui assure la convergence .
Do you follow me ? ... :zen:
Oui, c'est juste, je n'avais pas vu le carré sur la puissance.
On peut en fait appliquer d'Alembert en considérant la série comme une série usuelle de terme général

(ça a l'avantage de ne pas avoir à traiter
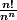
).
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 88 invités
tels que la suite
soit bornée ?
.

|x|^{n^2}=(n!)(|x|^n)^n<)
ce qui assure la convergence .