Bonjour
J'ai quitté les bancs de l'école depuis plusieurs années déjà (plus de 10 ans...) et mes vagues souvenirs de gradient et dérivés ne sont pas suffisants pour m'aider à solutionner un problème que j'ai aujourd'hui au boulot
Aussi, je vous remercie par avance de l'aide que vous pourrez m'apporter
soit la fonction f(x,y)
j'ai besoin de connaitre les dérivées df(x,y)/d(x) et df(x,y)/d(y) pour connaitre le gradient de f(x,y)-
--> jusque là, est-ce ok ?
si non, merci de m'éclairer sur la méthode pour obtenir les composantes du gradient de f(x,y)
si oui, merci de me dire comment procéder à la suite
En effet, la fonction f(x,y) est un peu complexe telle que :
f(x,y) = A * racine[ (B - x)^2 + (C - x)^2] + D * racine [ (E - y)^2 + (F - y)^2]
Et là, je me perds un peu dans tout ce bazar... avec les 1/( 2 * racine (...)) etc...
--> Est-ce que qqn pourrait m'aider SVP ?
Merci
Gradient et dérivées
6 messages
- Page 1 sur 1
Bonjour,
A mon sens, le difficulté d'un calcul de dérivée est la vérification. Donc on pourra confronter nos résultats.
f(x,y) = A * racine[ (B - x)^2 + (C - x)^2] + D * racine [ (E - y)^2 + (F - y)^2]
La dérivée partielle par rapport à x sera la dérivée du terme A * racine[ (B - x)^2 + (C - x)^2] seulement, puisque l'autre est constant.
Moi, j'écrirais f(x) = A * (BC -x(B+C) +x² )^1/2
Je vous rappelle que la dérivée de u^n est n*u^(n-1) * u'.
A mon sens, le difficulté d'un calcul de dérivée est la vérification. Donc on pourra confronter nos résultats.
f(x,y) = A * racine[ (B - x)^2 + (C - x)^2] + D * racine [ (E - y)^2 + (F - y)^2]
La dérivée partielle par rapport à x sera la dérivée du terme A * racine[ (B - x)^2 + (C - x)^2] seulement, puisque l'autre est constant.
Moi, j'écrirais f(x) = A * (BC -x(B+C) +x² )^1/2
Je vous rappelle que la dérivée de u^n est n*u^(n-1) * u'.
f(x,y) = A * racine[ (B - x)^2 + (C - x)^2] + D * racine [ (E - y)^2 + (F - y)^2]
Quand on cherche la dérivée partielle de f par rapport à x, y doit être considéré comme une constante.
Quand on cherche la dérivée partielle de f par rapport à y, x doit être considéré comme une constante
Et on applique alors, les "techniques" habituelles de dérivation.
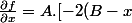 - 2(C-x)]/ [2.racine((B - x)^2 + (C - x)^2)])
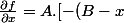 - (C-x)]/ [racine((B - x)^2 + (C - x)^2)])
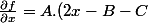/ [racine((B - x)^2 + (C - x)^2)])
et de manière analogue :
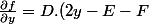/ [racine((E - y)^2 + (F - y)^2)])
:zen:
Quand on cherche la dérivée partielle de f par rapport à x, y doit être considéré comme une constante.
Quand on cherche la dérivée partielle de f par rapport à y, x doit être considéré comme une constante
Et on applique alors, les "techniques" habituelles de dérivation.
et de manière analogue :
:zen:
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 22 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
