Groupe linéaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 12 Déc 2012, 20:35
par barbu23 » 12 Déc 2012, 20:35
Bonjour à tous, :happy3:
Est ce que
 $)
et
 $)
sont des sous groupes de
 $)
.
Merci d'avance.
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 12 Déc 2012, 20:39
par Judoboy » 12 Déc 2012, 20:39
Problème ouvert, Gauss avait annoncé en avoir une démonstration mais elle ne rentrait pas dans la marge de son cahier. Depuis il est mort, et on cherche encore.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 12 Déc 2012, 20:40
par barbu23 » 12 Déc 2012, 20:40
Judoboy a écrit:Problème ouvert, Gauss avait annoncé en avoir une démonstration mais elle ne rentrait pas dans la marge de son cahier. Depuis il est mort, et on cherche encore.
Tu rigoles ? :ptdr:
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 12 Déc 2012, 20:47
par Judoboy » 12 Déc 2012, 20:47
Non non, y a un gros coup à jouer pour un chercheur un peu motivé.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 12 Déc 2012, 20:58
par barbu23 » 12 Déc 2012, 20:58
Judoboy a écrit:Non non, y a un gros coup à jouer pour un chercheur un peu motivé.
Il existe plusieurs cas de matrices :
 $)
telles que
 $)
mais :
 $)
. :hum:
-
Judoboy
- Membre Rationnel
- Messages: 654
- Enregistré le: 24 Fév 2012, 14:36
-
 par Judoboy » 12 Déc 2012, 21:08
par Judoboy » 12 Déc 2012, 21:08
barbu23 a écrit:Il existe plusieurs cas de matrices :
 $)
telles que
 $)
mais :
 $)
. :hum:
Comme par exemple ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 12 Déc 2012, 21:11
par barbu23 » 12 Déc 2012, 21:11
Judoboy a écrit:Comme par exemple ?
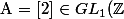 $)
implique que
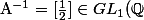 $)
.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 12 Déc 2012, 21:37
par leon1789 » 12 Déc 2012, 21:37
barbu23 a écrit:Bonjour à tous, :happy3:
Est ce que
 $)
et
 $)
sont des sous groupes de
 $)
.
Merci d'avance.
oui évidemment !

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 12 Déc 2012, 21:37
par leon1789 » 12 Déc 2012, 21:37
barbu23 a écrit: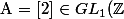 $)
ceci est faux car 2 n'est pas inversible dans Z.

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 12 Déc 2012, 21:39
par leon1789 » 12 Déc 2012, 21:39
Judoboy a écrit:Problème ouvert, Gauss avait annoncé en avoir une démonstration mais elle ne rentrait pas dans la marge de son cahier. Depuis il est mort, et on cherche encore.

Désolé d'avoir cassé ton histoire.
C'est pas joli de se moquer :ptdr: mais je te comprends
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 14 Déc 2012, 17:40
par barbu23 » 14 Déc 2012, 17:40
 $)
est - il un sous groupe de
 $)
?
Merci d'avance.
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 14 Déc 2012, 22:42
par ev85 » 14 Déc 2012, 22:42
barbu23 a écrit: $)
est - il un sous groupe de
 $)
?
Merci d'avance.
Bonsoir Pablo.
Peux-tu me rappeler quelles conditions doit vérifier un sous-groupe ?
-
Kikoo <3 Bieber
- Membre Transcendant
- Messages: 3814
- Enregistré le: 28 Avr 2012, 09:29
-
 par Kikoo <3 Bieber » 14 Déc 2012, 23:02
par Kikoo <3 Bieber » 14 Déc 2012, 23:02
barbu23 a écrit:Tu rigoles ? :ptdr:
C'est Fermat, mec, Fermat !
Pierre de Fermat a écrit:Il n'existe pas de triplet (x,y,z) de

tel que :
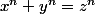
pour tout n entier supérieur ou égal à trois.
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Déc 2012, 01:26
par barbu23 » 15 Déc 2012, 01:26
ev85 a écrit:Bonsoir Pablo.
Peux-tu me rappeler quelles conditions doit vérifier un sous-groupe ?
Bonsoir @ev :
J'ai oublié ce fil, j'étais toute la journée sur l'autre forum.
Alors, pour que
 $)
soit un sous groupe, il faut que
 $)
:
 $)
et
 $)
.
J'ai posé cette question, parce que, je ne sais pas si

appartient ou non à
 $)
.
Merci d'avance. :happy3:
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 15 Déc 2012, 17:35
par ev85 » 15 Déc 2012, 17:35
barbu23 a écrit:Bonsoir @ev :
J'ai oublié ce fil, j'étais toute la journée sur l'autre forum.
Alors, pour que
 $)
soit un sous groupe, il faut que
 $)
:
 $)
et
 $)
.
J'ai posé cette question, parce que, je ne sais pas si

appartient ou non à
 $)
.
Merci d'avance. :happy3:
Peux-tu me donner une ou plusieurs méthodes pour calculer l'inverse d'une matrice ?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Déc 2012, 19:20
par barbu23 » 15 Déc 2012, 19:20
ev85 a écrit:Peux-tu me donner une ou plusieurs méthodes pour calculer l'inverse d'une matrice ?
Méthode de Cramer ?
-
ev85
- Membre Relatif
- Messages: 450
- Enregistré le: 08 Mar 2012, 14:23
-
 par ev85 » 15 Déc 2012, 19:30
par ev85 » 15 Déc 2012, 19:30
barbu23 a écrit:Méthode de Cramer ?
Excellent exemple. Que peux-tu dire des déterminants des matrices à coefficients dans

?
-
barbu23
- Membre Transcendant
- Messages: 5466
- Enregistré le: 18 Fév 2007, 17:04
-
 par barbu23 » 15 Déc 2012, 19:39
par barbu23 » 15 Déc 2012, 19:39
ev85 a écrit:Excellent exemple. Que peux-tu dire des déterminants des matrices à coefficients dans

?
Merci. :we:
Le calcul des déterminants ne fait intervenir que les

opérations élémentaires

, donc
 $)
.
Merci beaucoup. :lol3:
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
soit un sous groupe, il faut que
:
et
.
appartient ou non à
.