Exercice primitives

[pilousi]

Bonjour, je suis confronté à un exercice que je ne parviens pas à résoudre. Pourriez-vous m'aider ?
Merci beaucoup !

On pose sur R. étant continue, elle possède une primitive et en particulier telle que

1) Montrer que et en déduire que Déterminer k et en déduire que est impaire.

Je suis bloqué dès la première question mais si je considère je trouve k=0 Je ne comprends pas car on me demande de montrer que est impaire c'est à dire Si je remplace par 0 je trouve

2) On pose sur R*
Montrer que donc que

Je n'y parviens pas...

merci pour votre aide !

[Anonyme]

@pilousi

Pour info :

On n'écrit pas

car est un nombre et donc

il faut écrire :

ps)

Pistes de réflexions

1) Connais tu la fonction tangente ( tan ) ?
et sais tu que cette fonction est dérivable sur
et qu'on a sur cet intervalle

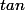
2) Sais tu que la fonction est une bijection de sur IR
et que sa fonction réciproque s'appelle
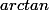
qui est une fonction dérivable sur IR et qu'on a :

[Anonyme]

@pilousi

Indication :

Si est une fonction continue sur un intervalle

cette fonction admet "DES primitives" sur cet intervalle qui sont des fonctions dérivables

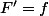
et on a sur cet intervalle

ps)
La fonction est une fonction paire sur IR

on a donc pour tout :

[Carpate]

Bonjour, je suis confronté à un exercice que je ne parviens pas à résoudre. Pourriez-vous m'aider ?
Merci beaucoup !

On pose sur R. étant continue, elle possède une primitive et en particulier telle que

1) Montrer que et en déduire que Déterminer k et en déduire que est impaire.

Je suis bloqué dès la première question mais si je considère je trouve k=0 Je ne comprends pas car on me demande de montrer que est impaire c'est à dire Si je remplace par 0 je trouve

2) On pose sur R*
Montrer que donc que

Je n'y parviens pas...

merci pour votre aide !

"Je ne comprends pas car on me demande de montrer que est impaire c'est à dire Si je remplace par 0 je trouve "
Si alors ou

2) avec

[Anonyme]

@Carpate

Merci d'expliquer pourquoi tu as écrit que ?

car je ne pense pas que c'est spécifié quelque part dans l'énoncé de cet exo ?

Dis moi si je me trompe ?

[Carpate]

@Carpate

Merci d'expliquer pourquoi tu as écrit que ?

car je ne pense pas que c'est spécifié quelque part dans l'énoncé de cet exo ?

Dis moi si je me trompe ?

Je répondais à Pilousi qui a écrit ... "je trouve F(x) = -F(-x)" et semblait ne pas voir que c'est équivalent à F(-x) = -F(x) et n'ai pas examiné sa démonstration sur le fond.
Mais ça n'offre aucune difficulté ..

[Anonyme]

@Carpate

On ne connait pas F mais f


Le seul truc qu'on sait sur la fonction F est une primitive de la fonction f et que F(0)=0

donc cela veut dire F'= f et F(0)=0



Pour calculer F'(-x)

il faut utiliser la formule de la dérivation d'une fonction composée car on a : F'(-x)= (F o u)' (x)

avec la fonction u définie par u(x)=-x
qui est une fonction dérivable sur IR et de fonction dérivée u'(x) = -1

ET Il suffit de conclure par un calcul qui est : .................

[pilousi]

Merci beaucoup pour vos réponses.

Pour la première question j'aboutis à la fin à donc c'est bien égal à
Je passe à la seconde !

[Anonyme]

@pilousi

Tu as du faire une faute de frappe car la question 1) demande de démontrer que -F'(-x)=f(x)

Et pour faire cette démo il suffit de calculer la fonction dérivée de la fonction définie par F(-X)
qui est une fonction composée de .....

ps)
Il faut bien sûr connaitre la formule du cours qui permet de calculer la fonction dérivée d'une fonction composée

[pilousi]

@pilousi

Tu as du faire une faute de frappe car la question 1) demande de démontrer que -F'(-x)=f(x)

Et pour faire cette démo il suffit de calculer la fonction dérivée de la fonction définie par F(-X)
qui est une fonction composée de .....

ps)
Il faut bien sûr connaitre la formule du cours qui permet de calculer la fonction dérivée d'une fonction composée

J'avais effectivement commis une faute de frappe. Merci !