Fonctions

[chameaubn]

Bonjour j'ai un exercice de maths assez complexe et noté à réalisé, pourriez-vous m'aider s'il vous plait, en voici l'énoncé :

on définit les fonctions f, g et hsur l'intervalle [0;1] par f(x)=;)x+1 (le tout sous la racine)
g(x)=1+x/2 et h(x)=1+x/2-x²/8
1. a. comparer (f(x))² et (g(x))²
b. en déduire que pour 02. a. montrer que, pour 0;)x;)1, h(x) est positif
b. comparer (f(x))² et (h(x))² sur l'intervalle [0;1]
c. en déduire que, pour 03.décrire les positions relatives des courbes représentatives des fonctions f, g et h
4.sans calculatrice, donner un encadrement de ;)1.000002
Quelle est l'amplitude de cet encadrement ? (l'amplitude de l'encadrement a
encore merci pour votre aide qui me sera très précieuse...

[Carpate]

Bonjour j'ai un exercice de maths assez complexe et noté à réalisé, pourriez-vous m'aider s'il vous plait, en voici l'énoncé :

on définit les fonctions f, g et hsur l'intervalle [0;1] par f(x)=;)x+1 (le tout sous la racine)
g(x)=1+x/2 et h(x)=1+x/2-x²/8
1. a. comparer (f(x))² et (g(x))²
b. en déduire que pour 0<x;)1, x+1<1+x/2
2. a. montrer que, pour 0;)x;)1, h(x) est positif
b. comparer (f(x))² et (h(x))² sur l'intervalle [0;1]
c. en déduire que, pour 0<x;)1.1+x/2-x²/8<;)x+1
3.décrire les positions relatives des courbes représentatives des fonctions f, g et h
4.sans calculatrice, donner un encadrement de 1.000002
Quelle est l'amplitude de cet encadrement ? (l'amplitude de l'encadrement a<y<b est le réel positif a-b)

encore merci pour votre aide qui me sera très précieuse...

Qu'as-tu déjà fait ?

[Anonyme]

@chameaubn

Comme on travaille sur l'intervalle [0;1] la fonction f définie par f(x)=;)x+1 est bien définie

La question 1) de cet exercice demande de calculer (f(x))²
on a donc : (f(x))² = (;)x+1)² = ......

puis demande de calculer (g(x))²
on a donc : (g(x))² = (1+x/2)² = ......

ET en "calculant le signe" de l'expression (g(x))² (f(x))²

tu dois pouvoir trouver que (f(x))² (g(x))² pour tout x de l'intervalle [0;1]


puis l'exercice demande de déduire que pour 0<x;)1 on a : x+1<1+x/2

Commentaire : Si dans une question , on demande "déduire" , c'est qu'il faut utiliser le résultat où les calculs de la question précédente...

ICI le résultat est : sur l'intervalle [0;1] on a : (;)x+1)² (1+x/2)²

Or comme la fonction "carré" ( c'est à dire la fonction définie par F(x)= x² )
est une fonction croissante pour tout x tel que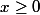

ET comme ici on travaille sur l'intervalle [0;1]
on a bien : pour tout x de l'intervalle [0;1]
x+1
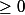
et 1+x/2

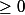
ET donc on peut écrire que pour tout x de l'intervalle [0;1]

SI on a : (;)x+1)² (1+x/2)² ALORS on a : x+1 ? 1+x/2

Conseil :
Peux tu , stp , faire ces différents calculs , et en cas de problème peux tu poser des questions plus précises sur les difficultés que tu rencontres (sur cette question ou les questions suivantes)

A+