Equation à résoudre
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Schabyne
- Membre Naturel
- Messages: 12
- Enregistré le: 22 Nov 2012, 12:56
-
 par Schabyne » 22 Nov 2012, 15:32
par Schabyne » 22 Nov 2012, 15:32
Manny06 a écrit:c'est parce que c'est 2^(x-3)=3^(y-1)
donc x=3 et y=1
Mais si on a:
"Justement, ici, tu as un entier N qui s'écrit
de cette manière
et de cette manière
Ce sont bien des factorisations est produit de nombres premiers (car 2 et 3 sont des nombres premiers) du même nombre N.
Or "The Famous Theorem" dit que cette factorisation est la même (unicité de la factorisation), ce qui implique x-3 = 0 et 0 = y en identifiant les exposants des nombres premiers 2 et 3. "y=0 ou y=1 car moi je lis après remplacement: 2^(3-3)=3^(0-1) soit 2^0=3^-1 avec y=1 c'est vrai que ça tombe juste, mais comment le trouve-t-on vu que d'après la décomposition en facteurs premiers y=0...

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 22 Nov 2012, 15:33
par leon1789 » 22 Nov 2012, 15:33
Manny06 a écrit:c'est parce que c'est 2^(x-3)=3^(y-1)
donc x=3 et y=1
oups, désolé, c'est moi qui est transformé un 3^(y-1) en 3^y. :triste:
Le principe reste bien sûr le même, et la réponse est donnée par Manny06

-
leon1789
- Membre Transcendant
- Messages: 5486
- Enregistré le: 27 Nov 2007, 15:25
-
 par leon1789 » 22 Nov 2012, 15:35
par leon1789 » 22 Nov 2012, 15:35
Schabyne a écrit:(...) moi je lis après remplacement: 2^(3-3)=3^(0-1) soit 2^0=3^-1 avec y=1 c'est vrai que ça tombe juste, mais comment le trouve-t-on vu que d'après la décomposition en facteurs premiers y=0...
Mais c'est
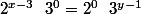
et là tu identifies les exposants respectivement pour 2 et 3, d'où x= ... et y=...
-
Schabyne
- Membre Naturel
- Messages: 12
- Enregistré le: 22 Nov 2012, 12:56
-
 par Schabyne » 22 Nov 2012, 15:38
par Schabyne » 22 Nov 2012, 15:38
leon1789 a écrit:Mais c'est
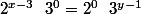
et là tu identifies les exposants respectivement pour 2 et 3, d'où x= ... et y=...
Ah ben oui, j'ai zappé ça je ne sais pas pourquoi, inattention surement!! grand merci a vous tous!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! je dois partir maintenant, je suis meme en retard mais merci encore a tous !! j'ai tout compris et c'est clair !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 113 invités
