Bonsoir, j'ai un petit soucis avec un exercice, j'espère vraiment que quelqu'un arrivera à m'aider :)
L'énoncé est:
Soit la fonction f(x,y) = (x² + y²)^(3/2)
1) Calculer ;)²f / ;)x²
Donc là j'ai trouvé: [3x² / (;)x²+ ;)y²)] + 3 (;)x²+ ;)y²)
2) On note r et ;) les coordonnées polaires, on définit la fonction g(r, ;)) = f(rcos;), rsin;))
Quelle est l'expression de g ? Donc là j'ai remplacé x et y par rcos ;) et rsin ;) et j'ai trouvé:
g= (r²)^(3/2)
Calculer ;)g/ ;)r, ;)g/ ;);) en déduire ;)f / ;)x
Alors là je commence à bloquer vu le g trouvé :/ sinon j'ai fait le calcul sans le g et j'ai trouvé
;)f / ;)x = ;)g/ ;)r * cos ;) - ;)g/ ;);)* (sin;)/r)
On notera cette fonction g1(r, ;))
Calculer ;)g1/ ;)r, ;)g1/ ;);), retrouver ;)²f / ;)x²
Et là je bloque (surement dû à des erreurs aux précédentes questions :/)
Je bloque depuis 3 bonnes heures sur cet exo, donc j'espère que quelqu'un arrivera à m'aider!! Merci beaucoup :)
Bonne soirée
Dérivées partielles
3 messages
- Page 1 sur 1
par C.Ret » 13 Nov 2012, 00:40
Bonsoir,
J'ai un petit souci, je ne trouva pas la même dériée partielle pour la question 1):
 = \left(x^2+y^2\right)^{\frac32})
J'utilise le fait que la dérivée de la fonction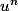
est de la forme 
:
=\frac{\partial }{\partial x}\left(x^2+y^2\right)^{\frac32}\\<br />\frac{\partial }{\partial x}f(x,y)=\frac32\frac{\partial }{\partial x}\left(x^2+y^2\right)\left(x^2+y^2\right)^{(\frac32-1)}\\<br />\frac{\partial }{\partial x}f(x,y)=\frac32\left(\frac{\partial }{\partial x}x^2+\frac{\partial }{\partial x}y^2\right)\left(x^2+y^2\right)^{\frac12}\\<br />\frac{\partial }{\partial x}f(x,y)=\frac32\left(2\frac{\partial x}{\partial x}x+2\frac{\partial y}{\partial x}y\right)\sqrt{x^2+y^2}\\<br />\frac{\partial }{\partial x}f(x,y)=\frac32\left(2x+0\right)\sqrt{x^2+y^2}\\<br />\frac{\partial }{\partial x}f(x,y)=3x\sqrt{x^2+y^2})
D'où
=\frac{\partial}{\partial x}3x\sqrt{x^2+y^2}\\<br />\frac{\partial^2}{\partial x^2}f(x,y)=\frac{\partial }{\partial x}(3x)\sqrt{x^2+y^2}+3x\frac{\partial }{\partial x}(\sqrt{x^2+y^2})\\<br />\frac{\partial^2}{\partial x^2}f(x,y)=3\frac{\partial x}{\partial x}\sqrt{x^2+y^2}+\frac{3x \frac{\partial }{\partial x}(x^2+y^2)}{2.\sqrt{x^2+y^2}}\\<br />\frac{\partial^2}{\partial x^2}f(x,y)=3\sqrt{x^2+y^2}+\frac{3x \left(\frac{\partial }{\partial x}x^2+\frac{\partial }{\partial x}y^2 \right)}{2.\sqrt{x^2+y^2}})
=3\sqrt{x^2+y^2}+\frac{3x ( 2x\frac{\partial x}{\partial x}+0 ) }{2.\sqrt{x^2+y^2}}\\<br />\frac{\partial^2}{\partial x^2}f(x,y)=3\sqrt{x^2+y^2}+\frac{6x^2}{2.\sqrt{x^2+y^2}}\\<br />\frac{\partial^2}{\partial x^2}f(x,y)=3\sqrt{x^2+y^2}+\frac{3.x^2}{\sqrt{x^2+y^2}}\\<br />\frac{\partial^2}{\partial x^2}f(x,y)=3\left(\sqrt{x^2+y^2}+\frac{x^2}{\sqrt{x^2+y^2}}\right ))
=3\left(\sqrt{x^2+y^2}+\frac{x^2}{\sqrt{x^2+y^2}}\right )\\<br />\frac{\partial^2}{\partial x^2}f(x,y)=3\left(\frac{x^2+y^2}{\sqrt{x^2+y^2}}+ \frac{x^2}{\sqrt{x^2+y^2}}\right )\\<br />\frac{\partial^2}{\partial x^2}f(x,y)=3\left( \frac{x^2+y^2\;+\;x^2}{\sqrt{x^2+y^2}}\right )\\<br />\frac{\partial^2}{\partial x^2}f(x,y)=3\left( \frac{2x^2+y^2}{\sqrt{x^2+y^2}} \right ))
Pour la question 2)
Je suis d'accord avec le resultat.L'expression se simplifie à la fin en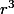
:
=f(r.cos\theta,r.sin\theta)\\<br />g(r,\theta )=\left ({(r.cos\theta )}^2+{(r.sin\theta )}^2\right )^{\frac32}\\<br />g(r,\theta )=\left (r^2.cos^2\theta +r^2.sin^2\theta \right )^{\frac32}\\<br />g(r,\theta )=\left (r^2.(cos^2\theta +sin^2\theta )\right )^{\frac32}\\<br />g(r,\theta )=\left (r^2.1\right)^{\frac32}\\<br />g(r,\theta )= {\left (r^2\right)}^{\frac32}\\<br />g(r,\theta )= {r}^{\frac{2\times3}2}\\<br />g(r,\theta)= r^3)
Pour la suite, je suis moi aussi un peu perplexe...
= \frac{\partial}{\partial r}r^3\\<br />\frac{\partial}{\partial r}g(r,\theta)= 3.\frac{\partial r}{\partial r}.r^{(3-1)}\\<br />\frac{\partial}{\partial r}g(r,\theta)= 3.r^2)
g ne semble pas être une fonction de
!
= \frac{\partial}{\partial \theta }r^3\\<br />\frac{\partial}{\partial \theta}\;g(r,\theta)= 3.\frac{\partial r}{\partial \theta }.r^{\left (3-1 \right )}\\<br />\frac{\partial}{\partial \theta}\;g(r,\theta)= 0)
??
Donc effectivement, il faut caculer les dérivées partielles à partir de la définition de g (et non du résultat précèdent).
=\frac{\partial }{\partial r}f(r.cos\theta,r.sin\theta )\\<br />\frac{\partial }{\partial r}g(r,\theta )=\frac{3}{2}.\frac{\partial }{\partial r}\left( (r.cos\theta )^2+(r.sin\theta )^2 \right).\left ( (r.cos\theta )^2+(r.sin\theta )^2 \right )^{\frac32-1}\\<br />\frac{\partial }{\partial r}g(r,\theta )=\frac{3}{2}.\frac{\partial }{\partial r}\left( r^2(cos^2\theta + sin^2\theta) \right).\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\\<br />\frac{\partial }{\partial r}g(r,\theta )=\frac{3}{2}.\frac{\partial }{\partial r}\left( r^2.1 <br />\right).\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\\<br />\frac{\partial }{\partial r}g(r,\theta )=\frac{3}{2}.\frac{\partial }{\partial r}r^2.\sqrt<br />{(r.cos\theta )^2+(r.sin\theta )^2}\\<br />\frac{\partial }{\partial r}g(r,\theta )=\frac{3}{2}.2.\frac{\partial r}{\partial r}.r.\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\\<br />\frac{\partial }{\partial r}g(r,\theta )=3.r.\sqrt{(r.cos\theta )^2+(r.sin\theta )^2})
Je retrouve donc bien une dérivée de même struture que la dérivée partielle de f. Mais non identique; on a bien x=r.cos O et y=r.sin O, mais r n'est pas x !
De même pour la dérivée partielle selon
\\<br />\frac{\partial }{\partial \theta}g(r,\theta )=\frac{3}{2}.\frac{\partial }{\partial \theta}\left( (r.cos\theta )^2+(r.sin\theta )^2 \right).\left ( (r.cos\theta )^2+(r.sin\theta )^2 \right )^{\frac32-1}\\<br />\frac{\partial }{\partial \theta}g(r,\theta )=\frac{3}{2}.\left (\frac{\partial }{\partial \theta}( r.cos\theta )^2\;+\;\frac{\partial }{\partial \theta}(r.sin\theta )^2 \right ).\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\\<br />\frac{\partial }{\partial \theta}g(r,\theta )=\frac{3}{2}.\left ((2r.cos\theta) \frac{\partial }{\partial \theta}\left( r.cos\theta \right)\;+\; (2r.sin\theta)\frac{\partial }{\partial \theta}\left( r.sin\theta \right) \right ).\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\\<br />\frac{\partial }{\partial \theta}g(r,\theta )=\frac{3}{2}.\left[ (2r.cos\theta) \left(\frac{\partial r}{\partial \theta}.cos\theta + r.\frac{\partial(cos\theta)}{\partial \theta}\right)\;+\;(2r.sin\theta)\left(\frac{\partial r}{\partial \theta}.sin\theta + r.\frac{\partial(sin\theta)}{\partial \theta}\right) \right].\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\\<br />\frac{\partial }{\partial \theta}g(r,\theta )=\frac{3}{2}.\left[ 2r.cos\theta (0 - r.sin \theta)\;+\; (2r.sin\theta) (0 + r.cos\theta ) \right].\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\\<br />\frac{\partial }{\partial \theta}g(r,\theta )=\frac{3}{2}.\left[ 2r^2.cos\theta.sin\theta\;-\; 2r^2.cos\theta.sin\theta \right].\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\\<br />\frac{\partial }{\partial \theta}g(r,\theta )=3.\left[ 0 \right].\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\\<br />\frac{\partial }{\partial \theta}g(r,\theta )=0)
J'ai beau tenter de tourner le problème dans tous es sens , j'arrive toujours au même résultat.
Telle que définie par l'énoncé, g n'est pas une fonction de
3) On pose donc
=3.r.\sqrt{(r.cos\theta )^2+(r.sin\theta )^2})
=\frac{\partial }{\partial r}\left(3.r.\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\right )\\<br />\frac{\partial }{\partial r}g1(r,\theta )=\frac{\partial }{\partial r}\left(3.r\right ).\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\;+\;3r.\frac{\partial }{\partial r}\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\\<br />\frac{\partial }{\partial r}g1(r,\theta )=3\frac{\partial r}{\partial r}.\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\;+\;3r.\frac{\frac{\partial }{\partial r}\left ((r.cos\theta )^2+(r.sin\theta )^2 \right )}{2.\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}}\\<br />\frac{\partial }{\partial r}g1(r,\theta )=3\left[\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\,+\,r.\frac{\frac{\partial }{\partial r}\left ((r.cos\theta )^2+(r.sin\theta )^2 \right )}{2.\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}}\right]\\)
=3\left[\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\,+\,r.\frac{\frac{\partial }{\partial r}\left (r^2(cos^2\theta+sin^2\theta)\right )}{2.\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}}\right]\\<br />\frac{\partial }{\partial r}g1(r,\theta )=3\left[\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\,+\,r.\frac{\frac{\partial }{\partial r}r^2}{2.\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}}\right]\\<br />\frac{\partial }{\partial r}g1(r,\theta )=3\left[\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\,+\,\frac{2r.\frac{\partial r}{\partial r}r}{2.\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}}\right]\\<br />\frac{\partial }{\partial r}g1(r,\theta )=3\left[\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}\,+\,\frac{r^2}{\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}}\right]\\)
=3\left[\frac{r^2+(r.cos\theta )^2+(r.sin\theta )^2}{\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}}\right]\\<br />\frac{\partial }{\partial r}g1(r,\theta )=3\left[\frac{(1+cos^2\theta+sin^2\theta)r^2}{\sqrt{(r.cos\theta )^2+(r.sin\theta )^2}}\right])
Je n'ai pas simplifier, en espèrant retrouver x et y.
On a bien une forme proche, mais non identique
Et dérivée par rapport à \théta :
Je trouve à nouveau 0.
Du coup, on peut simplifier:
=3\left[\frac{(1+1)r^2}{\sqrt{r^2.cos^\theta+r^2.sin^2\theta}}\right]\\\frac{\partial }{\partial r}g1(r,\theta )=3\left[\frac{2.r^2}{\sqrt{r^2}}\right]= 6.r)
Ce qui est bien la double dérivée de g.
J'espérais trouver quelque chose du genre
\;=\;\frac{\partial }{\partial r}g1(r,\theta )\,+\,\frac{\partial }{\partial \theta }g1(r,\theta ))
Cela m'inquiète...
... quelque chose nous échappe. :triste:
J'ai un petit souci, je ne trouva pas la même dériée partielle pour la question 1):
J'utilise le fait que la dérivée de la fonction
D'où
Pour la question 2)
Je suis d'accord avec le resultat.L'expression se simplifie à la fin en
Pour la suite, je suis moi aussi un peu perplexe...
g ne semble pas être une fonction de
Donc effectivement, il faut caculer les dérivées partielles à partir de la définition de g (et non du résultat précèdent).
Je retrouve donc bien une dérivée de même struture que la dérivée partielle de f. Mais non identique; on a bien x=r.cos O et y=r.sin O, mais r n'est pas x !
De même pour la dérivée partielle selon
J'ai beau tenter de tourner le problème dans tous es sens , j'arrive toujours au même résultat.
Telle que définie par l'énoncé, g n'est pas une fonction de
3) On pose donc
Je n'ai pas simplifier, en espèrant retrouver x et y.
On a bien une forme proche, mais non identique
Et dérivée par rapport à \théta :
Je trouve à nouveau 0.
Du coup, on peut simplifier:
Ce qui est bien la double dérivée de g.
J'espérais trouver quelque chose du genre
Cela m'inquiète...
... quelque chose nous échappe. :triste:
par Julietta » 13 Nov 2012, 13:17
Pour la dérivée partielle, certains trouvent 3r carré cos téta au lieu de r cube :/ mais je ne vois pas comment !!
En tout cas merci beaucoup, je vais essayer de manier ce que tu m'as dit :)
En tout cas merci beaucoup, je vais essayer de manier ce que tu m'as dit :)
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :