Equation diff.

par **kornflexx** » 08 Nov 2012, 14:53

Bonjour à tous,
Je me présente, je suis élève dans une écôle dingénieur en première année, et je rencontre beaucoup de difficulté en maths.
J'ai un devoir maison à rendre pour lundi suivant et deux exercices me pose vraiment problème, je ne comprend pas la démarche qu'il faut entreprendre pour les résoudre, je ne vois pas les étapes qu'il faut faire, enfaite je ne l'ai comprend pas.

le devoir maison:

Ce sont les exercices 2 et 3 qui me pose soucis.

Un grand merci à tous ceux qui m'aiderons, car je suis vraiment désespérer.
Bonne fin de journée :we: .

par **Arnaud-29-31** » 08 Nov 2012, 15:01

Bonjour,

Qu'as tu déjà fait ? Tu bloques dès la question 1 ?

par **kornflexx** » 08 Nov 2012, 15:05

Oui, enfin j'ai essayer de poser une nouvelle valeur de y en fonction de z grace à l'équation z=y'-2y et de remplacer les ancienne valeur de y dans l'équation (E), mais cela me donne une résultat avec des y et des z.

par **Arnaud-29-31** » 08 Nov 2012, 15:11

On a

et en dérivant

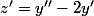
, on veut se ramener à l'équation (E).

Si l'on regarde simplement le premier terme de (E) :

, dans les expressions de

et

,on a du

que dans l'expression de

.
Il faut donc dans un premier temps regarder ce que donne

.

par **kornflexx** » 08 Nov 2012, 15:20

Merci beaucoup,

J'ai développé

sa me donne

Le soucis c'est que je ne comprend pas ta démarche, dans quel direction va-tu, quelles étapes compte tu faire pour résoudre cette question ? C'est cela que je ne comprend pas...

par **Arnaud-29-31** » 08 Nov 2012, 15:43

La démarche ici est simplement de faire apparaitre l'équation de départ on a que ça ...
Vu que l'on a

et

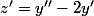
on voit que dans un premier temps pour faire apparaitre le premier terme on a aucun autre choix que de commencer notre équation en

par

.

Si tu préfères, tu peux dire

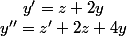
Puis tu remplaces y'' et y' dans l'équation de départ. C'est plus lourd mais la pas besoin d'avoir d'intuition, on fait ce qui est demandé sans réfléchir.

par **kornflexx** » 08 Nov 2012, 16:00

Ce coup je crois que j'ai compris :we:

Je suis parti sur tes bases:

Je suppose que c'est mon équation (E1), la question est donc fini ?

par **Arnaud-29-31** » 08 Nov 2012, 16:11

Oui, voilà c'est bien l'équation (

).

par **kornflexx** » 08 Nov 2012, 16:12

Je te remercie sincèrement pour ton aide, et je te souhaite une bonne fin de semaine :lol3:

par **Arnaud-29-31** » 08 Nov 2012, 16:21

De rien, bonne aprèm.

par **ti_math** » 08 Nov 2012, 17:42

Bonsoir, je voulais savoir s'il n'y avait pas une erreur dans l'exercice 3 car en fait je trouve les résultats suivant pour la question 1 :

z'(x)=(2ty+y') e^t²

z"(x)=e^t² (y"+4ty'+(4t²+2)y)

On remarque qu'avec z"(x) on est pas loin de l'équation de départ, or on a -4ty' dans léquation différentielle de départ et dans z"(x) on a +4ty', on remarque aussi qu'il faut rajouter y à z"(x).

N'y a t-il pas plutot un + à place du - dans (E), ce qui donnerait pour la question 1, z"+z=0

par **Arnaud-29-31** » 08 Nov 2012, 18:08

Je pense en effet qu'il y a une erreur d'énoncé.

par **Anonyme** » 09 Nov 2012, 11:37

Salut tout le monde,
J'ai les mêmes exercices à faire pendant les vacances.
Je suis rendu à la fin de l'exo 2 a la question 3, pour la question 2 j'ai trouvé a la fin que la solution générale est z(x) = (x + 3) (e^x + c)
Mais je ne vois pas ou mettre cette solution dans (E) pour finir sa résolution (de (E))
Sauf avec Essm (équation caractéristique) puis easm.
Merci d'avance pour celui qui réussira à me faire avancer.

Cdt

par **Anonyme** » 09 Nov 2012, 12:00

je trouve la même solution général que toi et ne vois pas non plus comment faire pour le 3) donc en théorie la solution général est bonne.

par **Kil56** » 09 Nov 2012, 12:04

Je suis d'accord aussi, et idem pour la 3)....

par **Anonyme** » 09 Nov 2012, 12:08

J'ai commencé comme ça pour la question 3 :
http://goo.gl/qdK2r

par **Anonyme** » 09 Nov 2012, 12:16

il me semble que tu n'utilise plus du tout la question 2 alors que daprès moi si il y a une question 1 et 2 c'est justement parce-quon ne peux résoudre(a notre niveau) autrement que par ce passage... Apres je peux me trompé :D

par **Anonyme** » 09 Nov 2012, 19:58

Petit up au cas où quelqu'un passerait par ici.

par **Anonyme** » 10 Nov 2012, 00:34

je pense avoir avancé un petit peu en gros on veux y et on sais que y'-2y=z donc en remplaçant on a y'-2y=(x+3)(e^x+C) qui est une équation différentielle du premier ordre a résoudre. Je me trompe?
Je trouve pour léquation y'-2y= 0 que les solutions sont de la forme Ke^(2x) avec K une constante différente de C par contre pour le second membre je vois pas trop comment faire...

Edit:j'ai intégré K'(x) j'ai divisé K(x)par e^2x et je trouve en solution général y=1/4(-C(2x+7)-4e^x(x+4))+Ke^(2x)
c'est ce que je devais trouvé?

Equation diff.

Equation diff.

Qui est en ligne