[Résolu] Equation diff. ordre 1 non lineaire, non exacte
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
MrPacane
- Membre Naturel
- Messages: 23
- Enregistré le: 27 Avr 2006, 03:39
-
par MrPacane » 22 Sep 2010, 17:24
Bonjour,
J'essaie de trouver les solutions (forme generale) de l'equation differentielle suivante :
\frac{dy}{dx}=0)
Nous avons vu en classe qu'il est possible de rendre exacte une equation differentielle de ce genre en la multipliant par un facteur d'integration
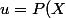Q(Y))
.
=\pm e^{\int p(x)dx})
=\pm e^{\int q(y)dy})
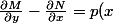N-q(y)M)
Cependant, l'integrale de q(y) n'est pas simple alors je me demandais si j'emploie la bonne technique... Y aurait-il un autre moyen de resoudre cette equation en passant par un autre chemin?
-
grikor
- Membre Naturel
- Messages: 30
- Enregistré le: 19 Mai 2009, 16:39
-
par grikor » 22 Sep 2010, 19:06
bonjour.
tu note y=z*x; y'=z'x+z
-
MrPacane
- Membre Naturel
- Messages: 23
- Enregistré le: 27 Avr 2006, 03:39
-
par MrPacane » 22 Sep 2010, 21:32
Après avoir fait la substitution, j'arrive à
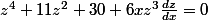
et donc
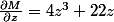
=\frac{\frac{\partial M}{\partial z}-\frac{\partial N}{\partial x}}{M}=\frac{22z-2z^3}{z^4+11z^2+30})
Comme
est fonction de
seulement, le facteur d'intégration
peut être trouvé à l'aide de la relation suivante :
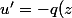u)
. C'est ce que j'ai tenté de faire, mais je me retrouve avec une intégrale assez complexe...
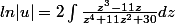
Quelqu'un voit où j'ai fait une erreur? :hein3:
-
grikor
- Membre Naturel
- Messages: 30
- Enregistré le: 19 Mai 2009, 16:39
-
par grikor » 23 Sep 2010, 11:13
bonjour.
-xdz/dx=(z^4+11z²+30)/(6z^3), équation séparable
int [6z^3/(z^4+11z²+30)]dz=int[6z/(z²+6)-(5z/(z²+5)]dz=-int dx/x
.......
-
MrPacane
- Membre Naturel
- Messages: 23
- Enregistré le: 27 Avr 2006, 03:39
-
par MrPacane » 23 Sep 2010, 13:11
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 37 invités
