Calcul de somme de series

[Adoniram]

C'est a dire que c'est ma premiere serie plus la seconde ie
avec et

[Adoniram]

??

[Le_chat]

Salut.

Je pense qu'étant donné l'énoncé, on n'attend pas une expression explicite de (an) en fonction de n, mais plutôt d'écrire, une fois le rayon de convergence trouvé: Si |x|<Rayon,


Et , on en déduit f(x).

Pour trouver le rayon sans calculer explicitement (an), on peut montrer par récurrence très facile que
, ce qui donne le rayon de 1/2.

Y a ptete des erreurs de calcul mais la méthode fonctionne.

[Anonyme]

@Le_chat

C'est vrai que ta méthode est super efficace pour calculer la fonction sans avoir besoin d'expliciter la suite

Question :
Est ce que tu pourrais un peu plus expliquer pourquoi l'énoncé te conduit à dire de ne pas expliciter la suite en fonction de n

[Le_chat]

Ben en fait quand on a une suite définie par récurrence, on aime bien utiliser la série génératrice associée, ne serait-ce que pour trouver une expression générale de la suite, vu que souvent la série génératrice vérifie une équation plutôt simple et donc on peut l'exprimer simplement.

Ici, comme on a une expression de (an) par récurrence, ben on voit que la série génératrice vérifie une relation pas trop compliquée. D'ailleurs dans la logique de l'énoncé, je pense que la question qui pourrait suivre serait: "en déduire une expression de (an) en fonction de n".

Pour ce faire, on dit que la série génératrice vérifie , on en déduit , on dse les deux membres et là on retrouve l'expression de (an) en fonction de n.

[Anonyme]

@Le_chat
Merci pour tes explictions et si j'ai bien compris ton raisonnement :

1) on démontre par un moyen quelconque (par exemple : théorème des gendarmes + récurrence) que le rayon de convergence de la série entière est

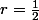
2) par unicité de la décomposition d'une série , si on pose

on arrive à idéntifier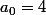 et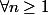

Ai-je bien compris le raisonnement ?

[Le_chat]

@Le_chat
Merci pour tes explictions et si j'ai bien compris ton raisonnement :

1) on démontre par un moyen quelconque (par exemple : théorème des gendarmes + récurrence) que le rayon de convergence de la série entière est

2) par unicité de la décomposition d'une série , si on pose

on arrive à idéntifier et

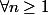
Ai-je bien compris le raisonnement ?

Oui c'est bien ça. Le point clé ici est de montrer que le rayon de convergence est non nul!

[Anonyme]

@Le_chat
Pourquoi non nul ?

[Le_chat]

Si il était nul, l'argument d'unicité du dse tombe à l'eau, on a besoin d'un rayon non nul.