Nature d'une série

[gamelle]

bonsoir,

je dois déterminer la nature des séries suivantes :

1)

alors pour ce faire j'ai modifié l'expression avec la quantité conjugué ce qui me donne


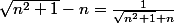
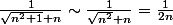
et (Riemann divergent)

donc par équivalence diverge

est ce que c'est correct???


2)

pour cette série j'ai utilisé le théorème de comparaison







( Riemann convergente)

donc par comparaison converge est ce que c'est correct aussi?

3)

la dernière j'ai beaucoup de mal à la faire j'ai essayé en multipliant deux encadrements



*
________________________________________


donc


or

(Riemann convergente)

ccl: la série est convergente

je ne sais pas si c'est possible de faire ce genre de chose en particulier la multiplication entre encadrements pouvez vous m'eclairez un peu plus



merci d'avance

[Pythales]

bonsoir,

je dois déterminer la nature des séries suivantes :

1)

alors pour ce faire j'ai modifié l'expression avec la quantité conjugué ce qui me donne


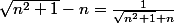
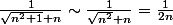
et (Riemann divergent)

donc par équivalence diverge

est ce que c'est correct???


2)

pour cette série j'ai utilisé le théorème de comparaison







( Riemann convergente)

donc par comparaison converge est ce que c'est correct aussi?

merci d'avance

Pour la 1 : oui
Pour la 2, tu peux utiliser Cauchy

[gamelle]

Pour la 1 : oui
Pour la 2, tu peux utiliser Cauchy

merci ^^
ben en fait on n'a pas vu Cauchy en cours

et sinon pour la 3) est ce que la multiplication des encadrements est correcte?? je ne sais pas trop comment on les utilise

[MMu]

merci ^^
ben en fait on n'a pas vu Cauchy en cours

et sinon pour la 3) est ce que la multiplication des encadrements est correcte?? je ne sais pas trop comment on les utilise

Je ne suis pas d'accord avec ton raisonnement pour la 3) !
As tu vu en cours les séries absolument convergentes ?
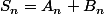
Sinon tu peux dire que avec = somme des termes positifs , = somme des termes négatifs,
et chacune des sommes converge (cf tes comparaisons)
:zen:

[gamelle]

Je ne suis pas d'accord avec ton raisonnement pour la 3) !
As tu vu en cours les séries absolument convergentes ?
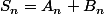
Sinon tu peux dire que avec = somme des termes positifs , = somme des termes négatifs,
et chacune des sommes converge (cf tes comparaisons)
:zen:

salut merci pour ta réponse oui j'ai bien étudié la convergence absolue mais je ne vois pas trop comment faire mais je faire essayer avec Sn=An+Bn

[MMu]

salut merci pour ta réponse oui j'ai bien étudié la convergence absolue mais je ne vois pas trop comment faire mais je faire essayer avec Sn=An+Bn

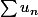
Avec la convergence absolue c'est immédiat : donc est convergente et donc est convergente .
:zen:

[mito94]

Sinon pense que cos(n) en valeur absolue est majorée par 1...
C'est très utile pour ce genre d'exercices

[gamelle]

ok ça marche merci pour l'aide