Le nombre d'or
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
mb511
- Messages: 8
- Enregistré le: 29 Oct 2012, 13:31
-
 par mb511 » 29 Oct 2012, 13:32
par mb511 » 29 Oct 2012, 13:32
Bonjour à tous.
Alors voilà, j'ai un exercice à faire pour la rentrée sauf que je n'y comprends absolument rien.
On cherche un rectangle particulier.
On veut le rapport

tel que si on retire un carré, dans le rectangle restant on ait le même rapport de sa longueur sur sa largeur.
1) Montrer que l'on doit avoir
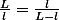
.
2) Montrer que

est solution de
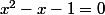
.
(avec

??)
3) Trouver

.
Voilà donc je ne sais pas comment commencer et je ne comprends pas bien l'énoncer.
Merci d'avance de votre aide.
-
ExarKun
- Membre Naturel
- Messages: 46
- Enregistré le: 28 Sep 2008, 00:28
-
 par ExarKun » 29 Oct 2012, 13:51
par ExarKun » 29 Oct 2012, 13:51
Bonjour,
La longueur est la côté le plus long d'un rectangle donc

.
Par conséquent je pense que quand tu dit qu'on enlève un carré c'est un carré de côté

(sinon on obtient plus un rectangle).
La relation de la question 1 en découle.
-
mb511
- Messages: 8
- Enregistré le: 29 Oct 2012, 13:31
-
 par mb511 » 29 Oct 2012, 13:53
par mb511 » 29 Oct 2012, 13:53
ExarKun a écrit:Bonjour,
La longueur est la côté le plus long d'un rectangle donc

.
Par conséquent je pense que quand tu dit qu'on enlève un carré c'est un carré de côté

(sinon on obtient plus un rectangle).
La relation de la question 1 en découle.
Oui c'est un carré de côté

mais je ne vois pas comment on peut trouver
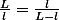
.
-
ExarKun
- Membre Naturel
- Messages: 46
- Enregistré le: 28 Sep 2008, 00:28
-
 par ExarKun » 29 Oct 2012, 14:01
par ExarKun » 29 Oct 2012, 14:01
Détails ce que tu as fait comme calcul.
-
mb511
- Messages: 8
- Enregistré le: 29 Oct 2012, 13:31
-
 par mb511 » 29 Oct 2012, 14:03
par mb511 » 29 Oct 2012, 14:03
ExarKun a écrit:Détails ce que tu as fait comme calcul.
Mais je sais pas comment faire. Je vois pas comment

peut être égal à

...
-
ExarKun
- Membre Naturel
- Messages: 46
- Enregistré le: 28 Sep 2008, 00:28
-
 par ExarKun » 29 Oct 2012, 14:05
par ExarKun » 29 Oct 2012, 14:05
Oui j'ai bien compris. Mais si tu n'arrives c'est que tu as bien essayé de faire quelque chose, non ?
-
mb511
- Messages: 8
- Enregistré le: 29 Oct 2012, 13:31
-
 par mb511 » 29 Oct 2012, 14:10
par mb511 » 29 Oct 2012, 14:10
ExarKun a écrit:Oui j'ai bien compris. Mais si tu n'arrives c'est que tu as bien essayé de faire quelque chose, non ?
En fait, j'ai fait un dessin (donc un rectangle avec comme côté l et un carré de côté l dans ce rectangle) donc j'ai bien compris le rapport

que l'on veut mais je n'arrive pas à comprendre pourquoi ce rapport il est égale à

.
Je pense savoir le démontrer avec des phrases mais pas par le calcul.
-
ExarKun
- Membre Naturel
- Messages: 46
- Enregistré le: 28 Sep 2008, 00:28
-
 par ExarKun » 29 Oct 2012, 14:14
par ExarKun » 29 Oct 2012, 14:14
Poses simplement les faits.
Après avoir retiré le carré, quelle est la longueur du rectangle ?
-
mb511
- Messages: 8
- Enregistré le: 29 Oct 2012, 13:31
-
 par mb511 » 29 Oct 2012, 14:21
par mb511 » 29 Oct 2012, 14:21
ExarKun a écrit:Poses simplement les faits.
Après avoir retiré le carré, quelle est la longueur du rectangle ?
Et bien L-l, il faut simplement expliquer cela avec des phrases ?
Il faut faire une démonstration alors ?
-
ExarKun
- Membre Naturel
- Messages: 46
- Enregistré le: 28 Sep 2008, 00:28
-
 par ExarKun » 29 Oct 2012, 14:27
par ExarKun » 29 Oct 2012, 14:27
mb511 a écrit:Et bien L-l, il faut simplement expliquer cela avec des phrases ?
Il faut faire une démonstration alors ?
Non il faut démontrer.
Si la longueur de ton nouveau rectangle est égal à

alors tu doit avoir
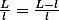
.
Est-ce que c'est possible ça ?
-
mb511
- Messages: 8
- Enregistré le: 29 Oct 2012, 13:31
-
 par mb511 » 29 Oct 2012, 14:30
par mb511 » 29 Oct 2012, 14:30
ExarKun a écrit:Non il faut démontrer.
Si la longueur de ton nouveau rectangle est égal à

alors tu doit avoir
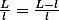
.
Est-ce que c'est possible ça ?
Ah non donc la longueur du nouveau rectangle c'est l et sa largeur c'est L - l ? Ce qui donne le rapport
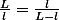
?
-
ExarKun
- Membre Naturel
- Messages: 46
- Enregistré le: 28 Sep 2008, 00:28
-
 par ExarKun » 29 Oct 2012, 14:31
par ExarKun » 29 Oct 2012, 14:31
Tout à fait :)
-
mb511
- Messages: 8
- Enregistré le: 29 Oct 2012, 13:31
-
 par mb511 » 29 Oct 2012, 15:03
par mb511 » 29 Oct 2012, 15:03
Ah merci beaucoup.
Je suis finalement arrivée à la question 3 en arrivant donc à l'équation
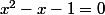
Donc j'ai résolu l'équation pour trouver la solution du rapport

mais là je rencontre deux problèmes (c'est peut-être normal mais je trouve ça bizarre).
Déjà il y a deux solutions (en calculant le discriminant delta est positif) c'est possible pour ce genre de rapport ?
De plus, les solutions sont
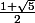
et
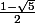
. Dois-je donner une approximation ou les laisser comme ça ?
-
ExarKun
- Membre Naturel
- Messages: 46
- Enregistré le: 28 Sep 2008, 00:28
-
 par ExarKun » 29 Oct 2012, 15:06
par ExarKun » 29 Oct 2012, 15:06
C'est normal qu'il y ait deux solutions.
Mais un rapport de longueur est positif, donc vis-à-vis de ton problème il ne faut donc garder que la valeur positive.
Sinon tes calculs sont corrects, tu viens de découvrir le nombre d'or :)
-
mb511
- Messages: 8
- Enregistré le: 29 Oct 2012, 13:31
-
 par mb511 » 29 Oct 2012, 15:12
par mb511 » 29 Oct 2012, 15:12
Ah merci beaucoup, en fait je me suis compliquée la vie pour le 1, le reste est logique.
Merci beaucoup. :D
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 224 invités
