Exercice DM
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
emilie1
- Messages: 8
- Enregistré le: 05 Oct 2012, 19:44
-
 par emilie1 » 05 Oct 2012, 19:47
par emilie1 » 05 Oct 2012, 19:47
Bonjour,
Enoncé: Soit F(x)= ax²+bx où a et b deux réels
1) determiner a et b en sachant que quelque soit x appartient à IR , F(x+1)-F(x)=x
2) Soit n un entier naturel. En utilisant la relation precedente : F(x+1)-F(x)=x pour n= 1;2;3;...;n
Montrer que: 1+2+3+...+n= F(n+1)-F(n)
3) En deduire la valeur de la somme des n premiers entiers naturels en fonction de n.
J'ai remplacé x par x+1 mais je n'arrive pas à continuer , si quelqu'un peut me donner la méthode pour resoudre cet exercice , ça serait vraiment gentil !
Merci d'avance.
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 05 Oct 2012, 20:07
par Arnaud-29-31 » 05 Oct 2012, 20:07
Bonsoir,
Après avoir remplacé

par
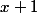
, tu as calculé ce que valait
 - F(x))
?
-
emilie1
- Messages: 8
- Enregistré le: 05 Oct 2012, 19:44
-
 par emilie1 » 05 Oct 2012, 20:10
par emilie1 » 05 Oct 2012, 20:10
J'ai trouvé a =1/2 et b=-1/2 mais apres je sais pas comment faire pour la 2 et 3

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 05 Oct 2012, 20:18
par chan79 » 05 Oct 2012, 20:18
emilie1 a écrit:J'ai trouvé a =1/2 et b=-1/2 mais apres je sais pas comment faire pour la 2 et 3
salut
complète puis ajoute membre à membre: (la somme de tout ce qui est à gauche est égale à la somme de tout ce qui est à droite)
F(2)-F(1)= ...
F(3)-F(2)= ...
F(4)-F(3)= ...
..
..
F(n+1)-F(n)= ...
-
emilie1
- Messages: 8
- Enregistré le: 05 Oct 2012, 19:44
-
 par emilie1 » 05 Oct 2012, 20:24
par emilie1 » 05 Oct 2012, 20:24
F(2)-F(1)= 1
F(3)-F(2)= 2
F(4)-F(3)= 3
F(n+1)-F(n)= 1
Est ce correcte ?
Aprés cela comment je fais ?
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 05 Oct 2012, 20:24
par Arnaud-29-31 » 05 Oct 2012, 20:24
On sait que
 - F(n) = n)
,
 - F(n-1) = n-1)
etc ...
C'est ce qu'il faut utiliser pour trouver une expression de
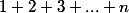
Tu as une erreur d'énoncé, il faut montrer
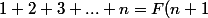-F(0))

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 05 Oct 2012, 20:28
par chan79 » 05 Oct 2012, 20:28
emilie1 a écrit:F(2)-F(1)= 1
F(3)-F(2)= 2
F(4)-F(3)= 3
F(n+1)-F(n)= 1
Est ce correcte ?
Aprés cela comment je fais ?
F(n+1)-F(n)=n
ajoute tout (il ya des simplifications)
-
emilie1
- Messages: 8
- Enregistré le: 05 Oct 2012, 19:44
-
 par emilie1 » 05 Oct 2012, 20:35
par emilie1 » 05 Oct 2012, 20:35
je trouve n(n+1)/2, qui fait (n^2+n)/2 , est ce correcte ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 05 Oct 2012, 21:38
par chan79 » 05 Oct 2012, 21:38
emilie1 a écrit:Comment je peux tous ajouter ? Je n'ai pas compris.
Arnaud, je trouve n(n+1)/2, ensuite ?
F(2)-F(1) + F(3)-(F2) + F(4)-F(3) + F(5)-F(5) +.....=1+2+3+...+n
après les simplifications, qu'est ce qui reste à gauche ?
-
emilie1
- Messages: 8
- Enregistré le: 05 Oct 2012, 19:44
-
 par emilie1 » 05 Oct 2012, 21:47
par emilie1 » 05 Oct 2012, 21:47
Ah oui , j'ai compris, merci. Ensuite je fais quoi ?

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 05 Oct 2012, 22:01
par chan79 » 05 Oct 2012, 22:01
emilie1 a écrit:Ah oui , j'ai compris, merci. Ensuite je fais quoi ?
tu trouves quoi ?
-
emilie1
- Messages: 8
- Enregistré le: 05 Oct 2012, 19:44
-
 par emilie1 » 06 Oct 2012, 11:43
par emilie1 » 06 Oct 2012, 11:43
Concernant, l'enoncé en effet, il y a une erreur mais mon professeur a dit que c'est : F(n+1)-F(1)
Je trouve : 1+2+3+...+n=(n+1)²/2-(n+1)/2 =(n²+n)/2=n(n+1)/2

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Oct 2012, 11:49
par chan79 » 06 Oct 2012, 11:49
emilie1 a écrit:Concernant, l'enoncé en effet, il y a une erreur mais mon professeur a dit que c'est : F(n+1)-F(1)
Je trouve : 1+2+3+...+n=(n+1)²/2-(n+1)/2 =(n²+n)/2=n(n+1)/2
c'est bien ce que tu dois trouver avec la méthode indiquée
-
emilie1
- Messages: 8
- Enregistré le: 05 Oct 2012, 19:44
-
 par emilie1 » 06 Oct 2012, 11:53
par emilie1 » 06 Oct 2012, 11:53
C'est à dire, parceque là je suis perdu :(
-
emilie1
- Messages: 8
- Enregistré le: 05 Oct 2012, 19:44
-
 par emilie1 » 06 Oct 2012, 12:05
par emilie1 » 06 Oct 2012, 12:05
Car je ne sais pas quoi faire avec ce resultat.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 06 Oct 2012, 17:00
par chan79 » 06 Oct 2012, 17:00
emilie1 a écrit:Car je ne sais pas quoi faire avec ce resultat.
le but de l'exercice c'est d'établir une formule qui donne le résultat de 1+2+3+...+n
tu as dû trouver F(n+1)-F(1)=1+2+3+ ... +n
or f(n)= an²+bn= 1/2 *(n²-n) car a=1/2 et b=-1/2
f(n+1)-f(1)=1/2((n+1)²-(n+1))-1/2(1-1)=1/2(n+1)(n+1-1)=
}{2})
donc 1+2+3+...+n=
}{2})
par exemple 1+2+3+ ... +999+1000=(1000*1001)/2=500500
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 30 invités
