Passer de f(x) = (x²-2x +1 / (1-x²) à f(x) = -1 +(2/1+x) ?
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Odessa
- Membre Naturel
- Messages: 18
- Enregistré le: 25 Avr 2012, 12:31
-
 par Odessa » 04 Oct 2012, 14:21
par Odessa » 04 Oct 2012, 14:21
Bonjour à tous. J'éspère que vous pourrez m'aider.
J'aimerais savoir comment on fait pour passer de :
f(x) = (x²-2x +1 / (1-x²) à f(x) = -1 +(2/1+x)
Merci beaucoup.
Odessa
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Oct 2012, 14:24
par Nightmare » 04 Oct 2012, 14:24
Hello,
par de la deuxième expression et réduit au même dénominateur.
On peut aussi faire le sens inverse, mais ça demande plus d'ingéniosité :
x²-2x+1=-(1-x²)-2x+2=-(1-x²)-2(x-1)
Donc x²-2x+1=-1-2(x-1)/(1-x²) puis 1-x²=(1-x)(1+x) donc 2(x-1)/(1-x²)=-2/(1+x) et on retombe bien sur nos pattes.

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 04 Oct 2012, 17:33
par chan79 » 04 Oct 2012, 17:33
Odessa a écrit:Bonjour à tous. J'éspère que vous pourrez m'aider.
J'aimerais savoir comment on fait pour passer de :
f(x) = (x²-2x +1 / (1-x²) à f(x) = -1 +(2/1+x)
Merci beaucoup.
Odessa
salut
tu as aussi
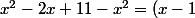^2}{(1-x)(1+x)}= - \fra{x-1}{x+1} = - \fra{(x+1)-2}{x+1}=-1 + \fra{2}{x+1})
-
tototo
- Membre Rationnel
- Messages: 954
- Enregistré le: 08 Nov 2011, 07:41
-
 par tototo » 04 Oct 2012, 18:46
par tototo » 04 Oct 2012, 18:46
chan79 a écrit:salut
tu as aussi
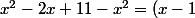^2}{(1-x)(1+x)}= - \fra{x-1}{x+1} = - \fra{(x+1)-2}{x+1}=-1 + \fra{2}{x+1})
Bonjour,
Les domaines de définitions de

et de

ne sont pas les meme R\{-1;1} et R\{-1}

-
chan79
- Membre Légendaire
- Messages: 10330
- Enregistré le: 04 Mar 2007, 19:39
-
 par chan79 » 04 Oct 2012, 19:17
par chan79 » 04 Oct 2012, 19:17
tototo a écrit:Bonjour,
Les domaines de définitions de

et de

ne sont pas les meme R\{-1;1} et R\{-1}
Bien-sûr !
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 04 Oct 2012, 19:20
par Nightmare » 04 Oct 2012, 19:20
tototo a écrit:Bonjour,
Les domaines de définitions de

et de

ne sont pas les meme R\{-1;1} et R\{-1}
Tout à fait, ça n'empêche pas l'égalité d'être vraie puisque dans ce sens on ne perd pas d'informations.
L'autre sens n'aurait été vrai qu'en précisant que x doit être différent de -1.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités
