Bonjour, je voudrais savoir comment faire pour déterminer les variations de la fonction
f(x) = (2x-2)/(x+1) et faire le tableau de variations. J'ai essayé, mais je ne comprend pas du tout comment je peux faire.
Merci de votre aide.
Odessa
Variation d'une fonction
11 messages
- Page 1 sur 1
Les variations
Pose f(x)= 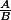 puis étudie d'abord séparément le signe de A et de B.
puis étudie d'abord séparément le signe de A et de B.
Alors on a f(x)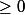 si A et B sont de même signe et f(x)
si A et B sont de même signe et f(x)  sinon.
sinon.
Quand f est-elle bien définie ? Quelle valeur interdite est à repérer ?
Alors on a f(x)
Quand f est-elle bien définie ? Quelle valeur interdite est à repérer ?
Deliantha a écrit:Pose f(x)=puis étudie d'abord séparément le signe de A et de B.
Alors on a f(x)si A et B sont de même signe et f(x)
sinon.
Quand f est-elle bien définie ? Quelle valeur interdite est à repérer ?
Attention Delantha, j'ai l'impression que tu confonds "tableau de signes" et "tableau de variations"
la fonction rationnelle
titine a écrit:Attention Delantha, j'ai l'impression que tu confonds "tableau de signes" et "tableau de variations"
Aucun impair car il s'agit de l'étude des variations d'une fonction quotient à partir de celle de son signe.
Salut,
la fonction est exprime comme une fraction de deux polynômes de degré 1. On appelle ces fonctions des fonctions homographiques. Pour déterminer les variations de f, quand tu auras vu les dérivées tu pourras calculer la dérivée de f. C'est une méthode générale. Mais dans cet exercice, on utilise une autre méthode, appelée décomposition en éléments simples, qui fonctionne avec toutes les fonctions homographiques.
Il suffit d'écrire astucieusement = \frac{2x-2}{x+1}=\frac{2(x+1)-4}{x+1}=2-\frac{4}{x+1}) . Et tu dois savoir si la fonction
. Et tu dois savoir si la fonction  est croissante ou décroissante, n'hésite pas pour cela à revenir à la définition d'une fonction croissante.
est croissante ou décroissante, n'hésite pas pour cela à revenir à la définition d'une fonction croissante.
la fonction est exprime comme une fraction de deux polynômes de degré 1. On appelle ces fonctions des fonctions homographiques. Pour déterminer les variations de f, quand tu auras vu les dérivées tu pourras calculer la dérivée de f. C'est une méthode générale. Mais dans cet exercice, on utilise une autre méthode, appelée décomposition en éléments simples, qui fonctionne avec toutes les fonctions homographiques.
Il suffit d'écrire astucieusement
Deliantha a écrit:Aucun impair car il s'agit de l'étude des variations d'une fonction quotient à partir de celle de son signe.
Je ne comprends pas ce que tu veux dire.
Une fonction négative peut être croissante ou décroissante.
Le signe d'une fonction n'a rien à voir avec ses variations.
titine a écrit:Je ne comprends pas ce que tu veux dire.
Une fonction négative peut être croissante ou décroissante.
Le signe d'une fonction n'a rien à voir avec ses variations.
Effectivement, une fonction peut-être positive croissante, positive décroissante, négative croissante, négative décroissante, et même ni croissante ni décroissante, etc.
En particulier, les fonctions homographiques sont monotones sur chacun des deux intervalles de leur ensemble de définition, et ce qui est intéressant ce n'est pas leur signe, c'est leur position relative par rapport a leur asymptote horizontale.
Variation de fonction homographiques
Luc a écrit:Effectivement, une fonction peut-être positive croissante, positive décroissante, négative croissante, négative décroissante, et même ni croissante ni décroissante, etc.
En particulier, les fonctions homographiques sont monotones sur chacun des deux intervalles de leur ensemble de définition, et ce qui est intéressant ce n'est pas leur signe, c'est leur position relative par rapport à leur asymptote horizontale.
J'allais dire ceci or le résumé est éloquent. La monotonie se déduit de limites par rapport aux asymptotes.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 62 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
