2nd degré fonctions

par **joh** » 05 Aoû 2012, 16:56

Bjr

J'aurai besoin d'aide pr cet exercice, j'en ais jamais fait de comme ça je sais pas comment m'y prendre. svp, merci d'avance

1) on a f(x)=ax²+15x+c trouver 2 réels a et c de telle sorte que f ait pr racines 4/3 et -1/2

2) g(x)=7x²+bx+2 , pr quelles valeurs a et b, g nadmet-elle pas de racine?

3) une fonction trinome admet un min egal a -1, cmb a-t-elle de racines?

4) une pelouse a la forme d-un rectangle dont la longeur est le double de la largeur, une allée de 3m de largeur l'entoure et l'air totale de la pelouse et de l'allée fait 360m².
Quelles sont les dimensions de la pelouse?

par **Dlzlogic** » 05 Aoû 2012, 17:24

Bonjour,
Pour le premier exercice, comment pourrait-on écrire cette fonction pour qu'elle admette les racines demandées ?

par **Deliantha** » 05 Aoû 2012, 17:53

1) Factorise f en utilisant f(4/3) et f(-1/2)
2) Calcule

. Qu'as-tu si

?
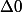
3) f'(-1)=0 d'où la variation de f
4) A=L*l avec L=2l d'où (L,l)

par **joh** » 05 Aoû 2012, 18:36

Deliantha a écrit:1) Factorise f en utilisant f(4/3) et f(-1/2)
2) Calcule . Qu'as-tu si ?
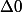
3) f'(-1)=0 d'où la variation de f
4) A=L*l avec L=2l d'où (L,l)

pour la Q1 : j'vois pas cmt j'px factoriser !

par **Kikoo <3 Bieber** » 05 Aoû 2012, 19:06

On factorise par les racines.
Cours : captain obvious

Et fais attention au language sms

par **joh** » 05 Aoû 2012, 19:43

Kikoo <3 Bieber a écrit:On factorise par les racines.
Cours : captain obvious

Et fais attention au language sms

Ok. 4/3(a²+15)+c ?? c'est trop compliqué , c'est pas ça?

par **Kikoo <3 Bieber** » 05 Aoû 2012, 19:58

Soit ax^2+bx+c=0 une equa quadratique.
Les solutions de cette equation, que l'on appelle les racines, sont x' et x''
ax^2+bx+c peut donc être transformé en (x-x')(x-x'')

par **joh** » 05 Aoû 2012, 20:05

Kikoo <3 Bieber a écrit:Soit ax^2+bx+c=0 une equa quadratique.
Les solutions de cette equation, que l'on appelle les racines, sont x' et x''
ax^2+bx+c peut donc être transformé en (x-x')(x-x'')

ah oui c'est vrai !!! merci
on a donc a(x+1/2)(x-4/3)

on developpe?

par **Kikoo <3 Bieber** » 05 Aoû 2012, 20:13

Exact :lol3:

par **joh** » 05 Aoû 2012, 20:17

Kikoo <3 Bieber a écrit:Exact :lol3:

ça donne a(x²-5/6x-2/3)

et les racines sont bien -1/2 et 4/3 c'est bon merci.

pour le b) on utilise a(x-x')² ??

par **Kikoo <3 Bieber** » 05 Aoû 2012, 20:36

J'ai approuvé trop vite : le a n'a aucune raison de figurer en facteur.
Désolé

Développe (x+ 1/2)(x- 4/3)

par **joh** » 05 Aoû 2012, 20:38

Deliantha a écrit:1) Factorise f en utilisant f(4/3) et f(-1/2)
2) Calcule . Qu'as-tu si ?
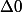
3) f'(-1)=0 d'où la variation de f
4) A=L*l avec L=2l d'où (L,l)

pour b) j'ai calculé

on a b²-56
si c'est plus petit que 0 aucune solution mais ça ne nous dit pas les valeurs

par **joh** » 05 Aoû 2012, 20:43

Kikoo <3 Bieber a écrit:J'ai approuvé trop vite : le a n'a aucune raison de figurer en facteur.
Désolé

Développe (x+ 1/2)(x- 4/3)

c'est bon ça marche merci

par **Kikoo <3 Bieber** » 05 Aoû 2012, 20:45

Si, pour le b), t'as une inéquation à résoudre, d'inconnue b.
Et il n'y a pas de coefficient a à trouver :hum:

par **joh** » 05 Aoû 2012, 22:58

Kikoo <3 Bieber a écrit:Si, pour le b), t'as une inéquation à résoudre, d'inconnue b.
Et il n'y a pas de coefficient a à trouver :hum:

bien sur mais ça fait 9, ya un probleme, est ce que c'est avec ou sans les x ? :/

par **Mimane37** » 06 Aoû 2012, 13:02

Je sais que ça a rien avoir mais je viens tout juste de m'inscrire et je compris absolument rien au forum et j'ai une question fin plusieurs questions ..
Je peux les poser ?

par **Dlzlogic** » 06 Aoû 2012, 13:14

Mimane37 a écrit:Je sais que ça a rien avoir mais je viens tout juste de m'inscrire et je compris absolument rien au forum et j'ai une question fin plusieurs questions ..
Je peux les poser ?

Bonjour,
Choisissez la section qui vous parait le plus appropriée (en cliquant sur "Maths-Forum"), et cliquez sur le gros bouton en haut à gauche : "Nouvelle discussion".

2nd degré fonctions

2nd degré fonctions

Qui est en ligne