Intégrale
6 messages
- Page 1 sur 1
Intégrale
Bonjour, je dois calculer l intégrale de la fonction f(x)=5(1-x)/racine (1-x^2) entre 1 et -1 mais je n arrive pas a trouver la primitive ... J'ai essayer en posant ce changement de variable t=1-x mais je bloque rapidement.. Est-t-il possible de faire une intégration par partie sur ce genre de fonction ?
Bonjour, remarques que =5*\sqrt{\frac{1-x}{1+x}})
Tu peux faire le changement de variable .
.
En exprimant en fonction de
en fonction de  , tu obtiens
, tu obtiens ^2}dx)
On obtient donc l'intégrale^2}=5\int_{0}^{+\infty}\frac{2u*2u}{(1+u^2)^2})
Une intégration par partie permet alors de calculer I en intégrant^2) et en dérivant
et en dérivant 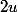 .
.
Le crochet est nul, le deuxième terme vaut*\int_{0}^{+\infty}\frac{2*(-1)}{1+u^2}=10 \int_{0}^{+\infty}\frac{1}{1+u^2}=5\pi) car
car  est la dérivée de l'arctangente.
est la dérivée de l'arctangente.
Tu peux faire le changement de variable
En exprimant
On obtient donc l'intégrale
Une intégration par partie permet alors de calculer I en intégrant
Le crochet est nul, le deuxième terme vaut
Probda18 a écrit:Bonjour, je dois calculer l intégrale de la fonction f(x)=5(1-x)/racine (1-x^2) entre 1 et -1 mais je n arrive pas a trouver la primitive ... J'ai essayer en posant ce changement de variable t=1-x mais je bloque rapidement.. Est-t-il possible de faire une intégration par partie sur ce genre de fonction ?
Black Jack a écrit:(1-x)/racine(1-x^2) = 1/racine(1-x^2) - x/racine(1-x^2)
et une primitive de 1/racine(1-x^2) est immédiate ... (arcsin...)
et une primitive de x/racine(1-x^2) est aussi immédiate ... (dérive racine(1-x^2) pour voir)
:zen:
Ça marche aussi :id: mais il faut quand même justifier que le crochet de
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
