Suites geometriques

[blonde]

Bonjour, j'ai besoin d'aide pour mon devoir . je ne suis arrivee qu'a la question 1a, le reste c'est la galere !
voila le sujet :

Soit une suite (Un)n definie pour tout entier naturel n, n>=2 par Un= (n-1)/(n+1)

1)a) Calculer les 3 premiers termes et le 25e terme de cette suite.
je trouve U2 = 1/3 U3 =1/2 et U4=3/5 U23= 11/12

b)exprimer en fonction de n, les termes U(n+1) et U(2n+1)
c) Etudier le sens de variation de la suite (Un)
d) demontrer que pour tout entier naturel n , n>=2 : 0

2) On considere la suite (Pn)n definie pour tout entier naturel n, n>=2 par : Pn= U2x U3x U4x ... xUn
a) Calculer les trois premiers termes de la suite (Pn)n
b) demontrer que la suite (Pn)n est decroissante .

Merci d'avance pr votre aide !

[el niala]

1a) pour moi, si la suite commence à U2, son 25ème terme n'est pas U23 mais... U26

1b) pour U(n+1) dans l'expression de Un remplace simplement n par n+1, même principe pour U(2n+1)

1c) c'est du cours, quel est le signe de U(n+1)-Un ?

1d) tu peux remarquer élégamment que

d'où la réponse

essaie de continuer

[blonde]

1a) pour moi, si la suite commence à U2, son 25ème terme n'est pas U23 mais... U26

1b) pour U(n+1) dans l'expression de Un remplace simplement n par n+1, même principe pour U(2n+1)

1c) c'est du cours, quel est le signe de U(n+1)-Un ?

1d) tu peux remarquer élégamment que

d'où la réponse

essaie de continuer

oui je ne men suis rendu compte quapres : ca donne U26 = 25/27

Mais je ny arrive aps ...

[blonde]

1a) pour moi, si la suite commence à U2, son 25ème terme n'est pas U23 mais... U26

1b) pour U(n+1) dans l'expression de Un remplace simplement n par n+1, même principe pour U(2n+1)

1c) c'est du cours, quel est le signe de U(n+1)-Un ?

1d) tu peux remarquer élégamment que

d'où la réponse

essaie de continuer

1b ) je trouve pour un+1= n/(n+2)
et pour u2n+2 =2n/(2n+2)

[blonde]

1a) pour moi, si la suite commence à U2, son 25ème terme n'est pas U23 mais... U26

1b) pour U(n+1) dans l'expression de Un remplace simplement n par n+1, même principe pour U(2n+1)

1c) c'est du cours, quel est le signe de U(n+1)-Un ?

1d) tu peux remarquer élégamment que

d'où la réponse

essaie de continuer

un+1 - un = 2/ (n+2)x(n+1)

est ce bon ?

svp aidez moi ... :mur:

[blonde]

1a) pour moi, si la suite commence à U2, son 25ème terme n'est pas U23 mais... U26

1b) pour U(n+1) dans l'expression de Un remplace simplement n par n+1, même principe pour U(2n+1)

1c) c'est du cours, quel est le signe de U(n+1)-Un ?

1d) tu peux remarquer élégamment que

d'où la réponse

essaie de continuer

mais je ne comprends pas coment a la 1d vs passez de n-1/n+1 à n+1)-1-1/n+1

[antonyme]

1b ) je trouve pour un+1= n/(n+2)
et pour u2n+2 =2n/(2n+2)

ça c'est bon, juste une erreur de frappe : c'est U(2n+1)
Et tu peux encore simplifier par 2

[maths0]

mais je ne comprends pas coment a la 1d vs passez de n-1/n+1 à n+1)-1-1/n+1

Non, je ne relirais pas pour savoir où tu en es ! Tu es en quelle classe ?

[blonde]

ça c'est bon, juste une erreur de frappe : c'est U(2n+1)
Et tu peux encore simplifier par 2

non , c'est 2n+1 et non 2n+2

[antonyme]

non , c'est 2n+1 et non 2n+2

Tu peux simplifier par 2 la fraction :lol3:

[antonyme]

un+1 - un = 2/ (n+2)x(n+1)

est ce bon ?

svp aidez moi ... :mur:

Oui c'est bon, que peut tu dire alors sur et ?

[blonde]

Tu peux simplifier par 2 la fraction :lol3:

ce qui fait n/n+1


apres jai trouve que Un est croissante, et je suis arrivee a demontrer que 0<un<1

Mais le 2 .... :mur:

[blonde]

Oui c'est bon, que peut tu dire alors sur et ?

au 2a :
P2 =u2
p3 = u2*u3
p4 = u2*u3*u4

bon ?

[blonde]

au 2a :
P2 =u2
p3 = u2*u3
p4 = u2*u3*u4

bon ?

pouvez vous mexpliquez comment proceder pour demontrer quelle est decroissante ..svp :hum:

[maths0]

au 2a :
P2 =u2
p3 = u2*u3
p4 = u2*u3*u4

bon ?

Oui ça ressemble !

[antonyme]

pouvez vous mexpliquez comment proceder pour demontrer quelle est decroissante ..svp :hum:

Pour trouver le sens de variation d'une suite, 3 méthode :
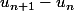
1 - Comparer à 0
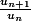
2 - Comparer à 1
3 - Par récurrence

Ici la méthode la plus adapté est la seconde.

[blonde]

Pour trouver le sens de variation d'une suite, 3 méthode :
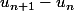
1 - Comparer à 0
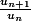
2 - Comparer à 1
3 - Par récurrence

Ici la méthode la plus adapté est la seconde.

donc si je fais le quotient, si c'est 1 croissant ? c'est ca ?


Merci bcp !

[antonyme]

donc si je fais le quotient, si c'est 1 croissant ? c'est ca ?


Merci bcp !

Yes! si est décroissante. Et inversement :lol3:

[el niala]

Yes! si est décroissante. Et inversement :lol3:

sans oublier de préciser que la suite en question est... positive, car sinon :triste:

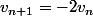
comme par exemple et

[blonde]

sans oublier de préciser que la suite en question est... positive, car sinon :triste:

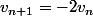
comme par exemple et

je trouve n²+n/n²+n+2

d'ou n²+n >= 6 >0
et n²+n+2 >= 8 >0

donc n²+n / n²+n+2 >0

or 0<6/8<1

donc 0< n²+n / n²+n+2< 1

d'ou Un+1 < Un donc 'Un est decroissante