Calcul d’un seul élément d’une matrice

[soft001]

Bonjour à vous tous,
J’ai une petite question sur la multiplication matricielle ;
One pose que j’ai plusieurs matrices A, B, C, D,…..

Code: Tout sélectionner

M=A*B*C*D*…
M=[m11   m12
 m21  m22 ]

je veux chercher l’élément m11 par exemple sans faire la multiplication des matrices.
Je sais bien que pour un produit simple des deux matrices on peut calculer élément par de la façon suivante :

si on augmente le nombre des matrice on fait comme ça :


Il n'y a pas une autre solution !!!!!!!!!!

[Skullkid]

Bonjour, en effet il n'y a pas d'autre écriture (en tout cas pas d'écriture "plus simple") en toute généralité le produit de plusieurs matrices. Après, si tu as un problème plus particulier, il y a peut-être des astuces envisageables...

[soft001]

Voici ce que je cherche à faire réellement :



Je veux trouvez d1, d2,... dn

n : [9 20]

Si n=10 : on va avoir 10 inconnus avec une seule équation.

[Skullkid]

Oui tu as plus d'inconnues que d'équations dès que tu as plus de 4 matrices à droite, donc a priori tu as avoir un grand espace de solutions (s'il y a des solutions), et je ne vois pas de façon de s'en sortir sans dérouler les calculs (réduire une des matrices n'a pas l'air de mener à grand-chose). On peut commencer par "tester" ton équation matricielle en vérifiant les déterminants : pour que ton système ait des solutions, il est nécessaire que .

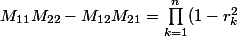[soft001]

Merci pour votre réponse,
En fait je ne connais que M11 et M21;
Par contre j'ai pas compris le r dans votre expression c'est le même dans ma expression ou bien quoi.

J'ai pensé à imposer arbitrairement n-1 équations supplémentaires, mais je pense que ça va pas marcher.

[Skullkid]

Si tu ne connais pas ta matrice M en entier oui ça réduit encore le nombre d'équations à ta disposition... Si tu imposes d'autres équations à côté, tu changes le problème. Oui les r_k dans mon écriture sont les mêmes que les tiens, j'ai écrit que le déterminant de M doit être égal au déterminant du produit des matrices inconnues.

[soft001]

J'ai une idée qui peut être va nous permettre d'augmenter le nombre des équations à notre disposition :
En faisant des approximations sur les valeurs de M11 et M21 pour chaque C1...n

Code: Tout sélectionner

(M11,M21)_1 pour C1
(M11,M21)_2 pour C2
...
(M11,M21)_n pour Cn

Après on va trouver plusieurs couples de solution on prend l'intersection des domaine de solution:

Code: Tout sélectionner

Solution{(M11,M21)_1 pour C1} intersection
Solution{(M11,M21)_2 pour C2} intersection
... intersection
Solution{(M11,M21)_n pour Cn}

Solution{(M11,M21)_1 pour C1} peut donner plusieurs couples de {d1..n}1, {d1..n}2,...