Exo intéressant

[newman]

Je profite de ma rare présence sur le forum pour poster un exo.
Soit M une matrice de Mn(C) et p supérieur ou égal à 1. Montrer que M est diagonalisable si et seulement si M^p estdiagonalisable et ker(M) = ker(M^p).

Bon courage

[ev85]

Je profite de ma rare présence sur le forum pour poster un exo.
Soit M une matrice de Mn(C) et p supérieur ou égal à 1. Montrer que M est diagonalisable si et seulement si M^p est diagonalisable et ker(M) = ker(M^p).

Bon courage

Bonjour Newman.

Le résultat est vrai pour un bloc de Jordan.

[newman]

Bonjour Newman.

Le résultat est vrai pour un bloc de Jordan.

ha je ne connaissais pas cette notion^^(au programme de maths spé?^^) mais oui tu as raison..

[Blueberry]

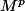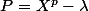Si on se place dans un sev propre F de pour une valeur propre , F est stable par et le polynôme annule .
Mais puisque , le polynôme a p racines distinctes.
Un polynôme a racines simples annule M sur F, donc M est diagonalisable sur F.
Puis M est diagonalisables sur tous les sev propres de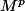 de valeurs propres non nulles.
Avec on conclut que M est diagonalisable.