Fonction terminale S
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 01 Avr 2012, 14:35
par globule rouge » 01 Avr 2012, 14:35
Azz a écrit:D'accord Mais A = 2 B = -2;)3m C = 3 c'est ça? Je trouve comment Delta en fonction de M alors?
eh bien vas-y, calcule Delta !

-
Azz
- Membre Naturel
- Messages: 37
- Enregistré le: 08 Oct 2010, 11:04
-
 par Azz » 01 Avr 2012, 14:40
par Azz » 01 Avr 2012, 14:40
( grâce à la calculatrice ! ) Dela = 456 X1 = 10.81 X2 = 0.13 ! donc deux solutions ! C'est bon? ( Et si c'est correct, une aide pour une reformulation de la question 5 merci ! )
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 01 Avr 2012, 14:47
par globule rouge » 01 Avr 2012, 14:47
Azz a écrit:( grâce à la calculatrice ! ) Dela = 456 X1 = 10.81 X2 = 0.13 ! donc deux solutions ! C'est bon? ( Et si c'est correct, une aide pour une reformulation de la question 5 merci ! )
Mais non, mais non !! ^^
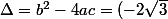^2-4(2\times 3))

Delta est une fonction de m, et on veut savoir quand Delta s'annule ! Nous résolvons une autre équation

-
Azz
- Membre Naturel
- Messages: 37
- Enregistré le: 08 Oct 2010, 11:04
-
 par Azz » 01 Avr 2012, 14:53
par Azz » 01 Avr 2012, 14:53
M² = 2
Dont M = -;)2 ou M = ;)2 .. On garde seulement M = ;)2 .. Ensuite? Je dois dire.. ? Qu'il existe deux solutions?.. Désolé ça sonne pas clair dans ma tête
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 01 Avr 2012, 14:57
par globule rouge » 01 Avr 2012, 14:57
Azz a écrit:M² = 2
Dont M = -;)2 ou M =

2 .. On garde seulement M =

2 .. Ensuite? Je dois dire.. ? Qu'il existe deux solutions?.. Désolé ça sonne pas clair dans ma tête
C'est un bon début

Delta s'annule pour

et

et est positif sur quels intervalles ? Il est négatif pour quels autres intervalles ?
PS : note que Delta est une fonction de m du second degré

-
Azz
- Membre Naturel
- Messages: 37
- Enregistré le: 08 Oct 2010, 11:04
-
 par Azz » 01 Avr 2012, 15:05
par Azz » 01 Avr 2012, 15:05
Alors ! Quand m ];)2; + linfini[ La fonction est positive !
Quand m];)2; - l'infini[ La fonction est positive !
Quand m ]-;)2;;)2[ La fonction est négative..
Je vois toujours pas comment faire pour trouver le nombre d'intersections..
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 01 Avr 2012, 15:09
par globule rouge » 01 Avr 2012, 15:09
Azz a écrit:Alors ! Quand m ];)2; + linfini[ La fonction est positive !
Quand m];)2; - l'infini[ La fonction est positive !
Quand m ]-;)2;;)2[ La fonction est négative..
Je vois toujours pas comment faire pour trouver le nombre d'intersections..
C'est très bien !!

Ben le nombre d'intersections est maintenant trivial ! Quand Delta est positif, il existe deux solutions réelles à l'équation, quand il est nul, il n'en existe qu'une seule et quand il est négatif, il n'y a pas de solutions réelles !
C'est tout !
-
Azz
- Membre Naturel
- Messages: 37
- Enregistré le: 08 Oct 2010, 11:04
-
 par Azz » 01 Avr 2012, 15:14
par Azz » 01 Avr 2012, 15:14
Mais oui!!!!! J'ai compris!!! Merci.. Est ce que tu pourrais maintenant à trouver une autre reformulation de la question 5 ? Montrer que lorsque m décrit l'intervalle ];)2;+l'inf[ , I décrit une partie, que l'on précisera, de la droite, d'équation y= (2/;)3)x.
-
globule rouge
- Membre Irrationnel
- Messages: 1011
- Enregistré le: 16 Fév 2012, 16:38
-
 par globule rouge » 01 Avr 2012, 15:33
par globule rouge » 01 Avr 2012, 15:33
Azz a écrit:Mais oui!!!!! J'ai compris!!! Merci.. Est ce que tu pourrais maintenant à trouver une autre reformulation de la question 5 ? Montrer que lorsque m décrit l'intervalle ];)2;+l'inf[ , I décrit une partie, que l'on précisera, de la droite, d'équation y= (2/;)3)x.
Euh, tu es sûr de l'équation de la droite ? :/
-
Azz
- Membre Naturel
- Messages: 37
- Enregistré le: 08 Oct 2010, 11:04
-
 par Azz » 01 Avr 2012, 16:03
par Azz » 01 Avr 2012, 16:03
J'ai relu.. et pardon.. j'ai compris aussi x =;)3/2y .. j'ai terminé! Merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 187 invités
2 .. On garde seulement M =
2 .. Ensuite? Je dois dire.. ? Qu'il existe deux solutions?.. Désolé ça sonne pas clair dans ma tête