Solution simplifiée

[donkey92]

Bonjour à tous :happy2: , je sollicite votre aide pour une simplification . Je vous explique au départ j'avais ce terme :

( LN(2) /3 )+(1/Racinede(3))*( 2*arctan (1/Racinede3)) et après essayé de simplifier au maximum j'en suis arrivé à :

(LN(2) * 2Racine(27) + 6pi ) / ( 3Racine(108))

mais voilà je n'en suis pas encore assez satisfait donc ma question est peut-on encore plus simplifié le terme précédent ?

Merci pour toutes réponses. :we:

[ev85]

Bonjour à tous :happy2: , je sollicite votre aide pour une simplification . Je vous explique au départ j'avais ce terme :

( LN(2) /3 )+(1/Racinede(3))*( 2*arctan (1/Racinede3)) et après essayé de simplifier au maximum j'en suis arrivé à :

(LN(2) * 2Racine(27) + 6pi ) / ( 3Racine(108))

mais voilà je n'en suis pas encore assez satisfait donc ma question est peut-on encore plus simplifié le terme précédent ?

Merci pour toutes réponses. :we:

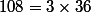
, non ?

[donkey92]

Merci pour ta réponse mais je cherche à simplifier l'ensemble :

(LN(2) * 2Racine(27) + 6pi ) / ( 3Racine(108))

en fait je cherche la solution exacte sous la forme la plus simplifiée possible

[ev85]

Merci pour ta réponse mais je cherche à simplifier l'ensemble :

(LN(2) * 2Racine(27) + 6pi ) / ( 3Racine(108))

en fait je cherche la solution exacte sous la forme la plus simplifiée possible

Je vais le dire autrement : simplifie ta fraction par 6.

[donkey92]

Merci beaucoup :) donc j'arrive donc à :


( ln(2)*racine(3)+pi ) / racine(27)

Ce qui me plaît déjà mieux :)

J'ai deux questions : comment avez-vous su , qu'il fallait diviser par 6 ?

est ce que vous pensez qu'il existe un quotient de racine égal à ln(2) ?

[ev85]

comment avez-vous su , qu'il fallait diviser par 6 ?

Parce que j'ai simplifié les racines carrées pardi ! Ce que je t'ai suggéré plus haut.

est ce que vous pensez qu'il existe un quotient de racine égal à ln(2) ?

Bonne question ! Une réponse sans intérêt est : oui. regarde : .
Si ta question est : existe-t-il des entiers naturels non nuls p et q tels que , je ne sais pas. Je pense que non. Je vais chercher du côté de l'artillerie lourde...

[Edit] Effectivement on ne peut pas. C'est de l'artillerie lourde . Il y a peut-être une démonstration plus élémentaire...

[Judoboy]

e.v. : ln(2) est transcendent, je pense que ça règle la question non ?

[ev85]

e.v. : ln(2) est transcendent, je pense que ça règle la question non ?

Oui, c'est ce que j'appelle de l'artillerie lourde. Tu as une démonstration élémentaire ?

[Judoboy]

Oui, c'est ce que j'appelle de l'artillerie lourde. Tu as une démonstration élémentaire ?

Mmhh après quelques recherches il se pourrait que la démonstration de ceci soit plus difficile que prévue

[donkey92]

Merci encore une fois pour ses explications détaillé.Je pense qu'on doit être arrivé à l'une des formes les plus simplifiées