Variations d'une fonction

[Pipioupiou]

Bonjour, je dois étudiez les variations de la fonctions f définie sur ]0;2] par

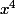
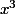
Je sais qu'il faut que je le fasse avec la derivée de cette fonction le problème est ue je n'arrive pas a la calculée, je me retrouve tout le temps avec des ou , et je ne sais pas comment analyser cela..

Merci d'avance :$

[chan79]

Bonjour, je dois étudiez les variations de la fonctions f définie sur ]0;2] par

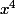
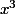
Je sais qu'il faut que je le fasse avec la derivée de cette fonction le problème est ue je n'arrive pas a la calculée, je me retrouve tout le temps avec des ou , et je ne sais pas comment analyser cela..

Merci d'avance :$

f(x) est de la forme u/v et tu as (u/v)'=(u'v-uv')/v²
ensuite, cherche à factoriser le numérateur

[Pipioupiou]

f(x) est de la forme u/v et tu as (u/v)'=(u'v-uv')/v²
ensuite, cherche à factoriser le numérateur

OUi, oui, ca s'est fait, je le sais, c'est le calul auquel je n'arrive pas..

J'ai calculé la dérivée de u, qui est u'=4x(x²+4)
et la derivée de v, qui est v' = 4

Je suis donc rendue a :


Mais a partir de la je ne sais plus quoi faire, pour que ma fonctions reste avec des x² et pas autres chose que je ne sais pas analysée..

[chan79]

OUi, oui, ca s'est fait, je le sais, c'est le calul auquel je n'arrive pas..

J'ai calculé la dérivée de u, qui est u'=4x(x²+4)
et la derivée de v, qui est v' = 4

Je suis donc rendue a :


Mais a partir de la je ne sais plus quoi faire, pour que ma fonctions reste avec des x² et pas autres chose que je ne sais pas analysée..

il faut factoriser 4(x²+4)²-4(x²+4)²
attention, j'ai remis une parenthèse au bon endroit

[Pipioupiou]

il faut factoriser 4(x²+4)²
attention, j'ai remis une parenthèse au bon endroit

Mais comment factorisé justement ?

[chan79]

Mais comment factorisé justement ?

c'est simplement la distributivité

4(x²+4)[4x²-(x²+4)]

[Pipioupiou]

c'est simplement la distributivité

4(x²+4)[4x²-(x²+4)]

Je ne comprends pas, on parle bien du deuxième terme du numerateur ?

Comment peux t'on passer de ça 4(x²+4)² à ça 4(x²+4)[4x²-(x²+4)] ?

[gaga2012]

Développe et réduit ta dérivé après simplifie par 4

Tu obtiendras une fraction polynomiale bicarré et il te suffit de poser X=x^2 et tu étudiera ta le signe de ta dérivé avec X positive puisque X=x^2

essaye de proposer quelque chose avec ces indications et je t'aiderai encore plus

Du courage!!!!

[chan79]

Je ne comprends pas, on parle bien du deuxième terme du numerateur ?

Comment peux t'on passer de ça 4(x²+4)² à ça 4(x²+4)[4x²-(x²+4)] ?

c'est le numérateur de la dérivée qu'on factorise

[Pipioupiou]

Développe et réduit ta dérivé après simplifie par 4

Tu obtiendras une fraction polynomiale bicarré et il te suffit de poser X=x^2 et tu étudiera ta le signe de ta dérivé avec X positive puisque X=x^2

essaye de proposer quelque chose avec ces indications et je t'aiderai encore plus

Du courage!!!!

Oh oui, il m'en faut du courage

Mais c'est justement reduire et simplifier que je n'arrive pas a faire :
J'arrive à :

MAis après je ne sais plus quoi faire..

[chan79]

Oh oui, il m'en faut du courage

Mais c'est justement reduire et simplifier que je n'arrive pas a faire :
J'arrive à :

MAis après je ne sais plus quoi faire..

tu mets 4(x²+4) en facteur dans 4x(x²+4)*4x-4(x²+4)²

[Pipioupiou]

tu mets 4(x²+4) en facteur dans 4x(x²+4)*4x-4(x²+4)²

D'accord !!
J'ai compris !
Mais arrivée ici, que dois je faire ? :$
J'ai mainteannt :



Je divise tout par 4 ce qui me donnerait :

?

[Pipioupiou]

D'accord !!
J'ai compris !
Mais arrivée ici, que dois je faire ? :$
J'ai mainteannt :



Je divise tout par 4 ce qui me donnerait :

?

Ce n'est pas ça ? :$

[gaga2012]

Ce n'est pas ça ? :$

Non tu as mal simplifier!!!!!

pourquoi simplifies tu le 4 qui se trouve dans la somme (4x^2-(x^2+4))? ça ne se fait pas!

[Pipioupiou]

Non tu as mal simplifier!!!!!

pourquoi simplifies tu le 4 qui se trouve dans la somme (4x^2-(x^2+4))? ça ne se fait pas!

Oups, j'ai pas fait attention :$

Mais comment je fais pour continuer, ma resolution ? :$

[gaga2012]

Ce n'est pas ça ? :$

Tu obtiens par contre pour en finir avec

(x^2+4)(4x^2-(x^2+4))/(4x^2)

et en reduisant le deuxieme facteur du numérateur tu as

(x^2+4)(3x^2-4)/(4x^2)

Après tu étudies le signe de la dérivée qui dépend seulement du signe de 3x^2-4 car x^2+4>0 et 4x^2>0 pour tous réels

Alors tu peux finir l'exo!!!!!

Si tu avait développer depuis le debut je t'aurai proposer de poser X=x^2 mais comme quelqu'un t'a proposé de factoriser ( ce qui est génial de sa part!!!!), poser X=x^2 n'est plus necessaire

[chan79]

Bonjour, je dois étudiez les variations de la fonctions f définie sur ]0;2] par

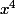
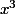
Je sais qu'il faut que je le fasse avec la derivée de cette fonction le problème est ue je n'arrive pas a la calculée, je me retrouve tout le temps avec des ou , et je ne sais pas comment analyser cela..

Merci d'avance :$

Je ne vois vraiment pas la difficulté en factorisant le numérateur de cette dérivée. On obtient
4(x²+4)(3x²-4)
Aucun intérêt à poser X=x²

[gaga2012]

@chan 79

moi en developpant depuis le debut j'ai trouvé la forme developper de ta facto et pour étudier le signe il me fallait poser X=x^2 car c'est un polynome bicarré. Toi tu as eu le coup d'oeuil de factoriser directement et tu as raison ya aucune difficulté, il faut néanmoin voir d'abord!!!!!!!!!!!

[chan79]

@chan 79

moi en developpant depuis le debut j'ai trouvé la forme developper de ta facto et pour étudier le signe il me fallait poser X=x^2 car c'est un polynome bicarré. Toi tu as eu le coup d'oeuil de factoriser directement et tu as raison ya aucune difficulté, il faut néanmoin voir d'abord!!!!!!!!!!!

En règle générale, il vaut mieux conseiller aux élèves de factoriser, même si dans certains cas, on y arrive en développant.
Bonne soirée