Problème sur les dérivés...
24 messages
- Page 1 sur 2 - 1, 2
Problème sur les dérivés...
Bonjour,
J'ai un DM à rendre pour lundi et je suis vraiment bloquée à une question. Ça fait trois heures que je suis dessus, en vain...
f est la fonction définie sur R par f(x)=3x²+1 / x-4 (je précise que le / est la barre fractionnaire)
1. Calculer le taux d'accroissement de f entre les réels 3 et 3+h.
2. La fonction f est-elle dérivable en a=3 ? Si oui, que vaut f'(3) ?
3. La fonction f est-elle dérivable en a=4 ?
Pour la question 1), j'ai fait :
En développant cette formule, j'arrive à :
Est-ce bon ?
Pour la 2, je ne sais pas comment m'y prendre pour savoir si a est dérivable en 3.
Dois-je reprendre la formule précédente ou faire :
[3(3+h)²+1 / (3+h)-4] / h ?
Je ne comprends vraiment pas cette question...
Qui peut m'aider ? :triste:
Merci et bonne soirée à tous !
J'ai un DM à rendre pour lundi et je suis vraiment bloquée à une question. Ça fait trois heures que je suis dessus, en vain...
f est la fonction définie sur R par f(x)=3x²+1 / x-4 (je précise que le / est la barre fractionnaire)
1. Calculer le taux d'accroissement de f entre les réels 3 et 3+h.
2. La fonction f est-elle dérivable en a=3 ? Si oui, que vaut f'(3) ?
3. La fonction f est-elle dérivable en a=4 ?
Pour la question 1), j'ai fait :
En développant cette formule, j'arrive à :
Est-ce bon ?
Pour la 2, je ne sais pas comment m'y prendre pour savoir si a est dérivable en 3.
Dois-je reprendre la formule précédente ou faire :
[3(3+h)²+1 / (3+h)-4] / h ?
Je ne comprends vraiment pas cette question...
Qui peut m'aider ? :triste:
Merci et bonne soirée à tous !
LaPtiteLuna a écrit:Bonjour,
J'ai un DM à rendre pour lundi et je suis vraiment bloquée à une question. Ça fait trois heures que je suis dessus, en vain...
f est la fonction définie sur R par f(x)=3x²+1 / x-4 (je précise que le / est la barre fractionnaire)
1. Calculer le taux d'accroissement de f entre les réels 3 et 3+h.
2. La fonction f est-elle dérivable en a=3 ? Si oui, que vaut f'(3) ?
3. La fonction f est-elle dérivable en a=4 ?
Pour la question 1), j'ai fait :
f(3+h)-f(3) / h = [(3(3+h)²+1 / (3+h)-4) - (3*3²+1 / 3-4)] / h
En développant cette formule, j'arrive à : 3h+46 / h-1.
Est-ce bon ?
Pour la 2, je ne sais pas comment m'y prendre pour savoir si a est dérivable en 3.
Dois-je reprendre la formule précédente ou faire :
[3(3+h)²+1 / (3+h)-4] / h ?
Je ne comprends vraiment pas cette question...
Qui peut m'aider ? :triste:
Merci et bonne soirée à tous !
Bonsooir
Par définition, une fonction est dérivale en un réel a ssi
Julie
De la dérivabilité de f
f est dite dérivable en 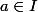 si elle admet une dérivée en a. La dérivabilité se montre par ces 2 moyens :
si elle admet une dérivée en a. La dérivabilité se montre par ces 2 moyens :
- localement (en un ou plusieurs points): par l'existence d'une dérivée à l'aide de limites.
Il existe une application de
de  dans
dans  telle que
telle que  de
de  :
:=\lim_{x\to a}\frac{f(x)-f(a)}{x-a} \Longleftrightarrow f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}h)
- globalement, on montre par propriétés de dérivées que est l'assemblage de fonctions dérivables sur
est l'assemblage de fonctions dérivables sur  .
.
- localement (en un ou plusieurs points): par l'existence d'une dérivée à l'aide de limites.
Il existe une application
- globalement, on montre par propriétés de dérivées que
La dérivabilité en un point
Le calcul du 1) ma paraît incorrect (gare aux parenthèses à appliquer à propos et comme il se doit).
Si la limite du taux d'accroissement existe au point d'absisse fixé, alors la dérivée existe en ce point.
Rien n'empêche par ailleurs d'employer une table déjà connue d'un ensemble des dérivées usuelles.
Si la limite du taux d'accroissement existe au point d'absisse fixé, alors la dérivée existe en ce point.
Rien n'empêche par ailleurs d'employer une table déjà connue d'un ensemble des dérivées usuelles.
Elerinna a écrit:Le calcul du 1) ma paraît incorrect (gare aux parenthèses à appliquer à propos et comme il se doit).
Si la limite du taux d'accroissement existe au point d'absisse fixé, alors la dérivée existe en ce point.
Rien n'empêche par ailleurs d'employer une table déjà connue d'un ensemble des dérivées usuelles.
Pour la 1, je peux peut-être poster tout le calcul pour vérifier ? Car je ne vois pas autre chose que ça...
J'ai donc fait à partir de ma formule...
Je ne vois pas autre chose... :triste:
LaPtiteLuna a écrit:Bonjour,
J'ai un DM à rendre pour lundi et je suis vraiment bloquée à une question. Ça fait trois heures que je suis dessus, en vain...
f est la fonction définie sur R par f(x)=3x²+1 / x-4 (je précise que le / est la barre fractionnaire)
1. Calculer le taux d'accroissement de f entre les réels 3 et 3+h.
2. La fonction f est-elle dérivable en a=3 ? Si oui, que vaut f'(3) ?
3. La fonction f est-elle dérivable en a=4 ?
Pour la question 1), j'ai fait :
f(3+h)-f(3) / h = [(3(3+h)²+1 / (3+h)-4) - (3*3²+1 / 3-4)] / h
En développant cette formule, j'arrive à : 3h+46 / h-1.
Est-ce bon ?
Pour la 2, je ne sais pas comment m'y prendre pour savoir si a est dérivable en 3.
Dois-je reprendre la formule précédente ou faire :
[3(3+h)²+1 / (3+h)-4] / h ?
Je ne comprends vraiment pas cette question...
Qui peut m'aider ? :triste:
Merci et bonne soirée à tous !
OK pour (3h+46)/(h-1)
s'il y a une limite finie quand h tend vers 0, il y a dérivabilité
Elerinna a écrit:La tienne reste suffisante dans le cadre de la définition initiale : applique encore la limite
Je ne vois vraiment pas comment je pourrais faire après... La limite est finie donc f est dérivable en a, et comme a=3 la fonction est dérivable en 3 c'est ça ?
Après je vois pas du tout comment je peux calculer f'(a)...
LaPtiteLuna a écrit:Sinon est-ce que je dois mettre ça pour la question 2 :
f'(a)=lim h-> 0
La limite est finie donc f est dérivable en a=3.
Si h tend vers 0,tend vers 46.
f'(x) = 3
f'(3) = 3
C'est ça ?
C'est presque ça en fait
On montre cependant que cette limite est égale au nombre dérivé de la fonction en a donc
Dans ton cas, tu as trouvé que
Julie
globule rouge a écrit:C'est presque ça en faitsauf que je te ramène aux messages précédents, une fonction est dérivable localement en un réel a si l'accroissement local en a est un réel quand h devient de plus en plus petit, c'est-à-dire si
. Ici, rien de nouveau ! ^^
On montre cependant que cette limite est égale au nombre dérivé de la fonction en a donc, comme l'a dit Elerinna.
Dans ton cas, tu as trouvé quedonc
!
Julie
Ahhhhhh :we: Il fallait juste remplacer le h par 0.
Merci beaucoup, j'ai bien compris !
globule rouge a écrit:bah vi =) h devient négligeable quand il tend vers 0, donc on peut le "considérer" nul même s'il ne l'est pas vraiment !
Je suis ravie que tu aies compris ! :++:
D'accord, merci encore !
La troisième (et dernière) question est la même que la 2) avec a=4, ça devrait être plus facile vu que j'ai compris le principe !
DM de math
bonjour, j'ai un DM a rendre pour demain et je bloque vraiment ! voici l'enoncé :
f et g sont les fonctions définies sur R par:
f(x)= (3x²+5x-1)/(x²+1) et g(x)= (5x-4)/(x²+1)
--> Démontrer que pour tout nombre réel x , f'(x) = g'(x) sans calculer ces deux dérivées.
Vous pouvez m'aider ? :/
f et g sont les fonctions définies sur R par:
f(x)= (3x²+5x-1)/(x²+1) et g(x)= (5x-4)/(x²+1)
--> Démontrer que pour tout nombre réel x , f'(x) = g'(x) sans calculer ces deux dérivées.
Vous pouvez m'aider ? :/
24 messages
- Page 1 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
