Exponentielle

par **Neijin46** » 01 Fév 2012, 16:07

Bonjour, j'ai un soucis,on me demande de faire ça
g(x) = (ex+1)(2ex-1)
Justifier que g(x) est du signe de 2ex-1. En déduire que g(x)>0 pour x >-ln2 et g (x)< ou égale pour x < ou égale a -ln2.
voila ce que j'ai répondu,
Pour tout réel x, ex>0 car une exponentielle est toujours positive et 1>0 donc g(x) est du signe de 2ex-1.
La j'ai justifié que g(x) était du signe de 2ex-1. Ensuite j'en déduis que g(x)>0 pour x >-ln2 et g (x)< ou égale pour x < ou égale a -ln2 avec les inéquations ci-dessous
2ex-1>0 ex+1>0
2ex > 1 ex>-1
ex > 1/2
ln(ex) > ln(1/2) Impossible car une exponentielle est toujours positive
x >ln1-ln(2)
x>-ln2

Donc S=-ln2 ( entre acolade)

2ex-1= <0
2ex= < 1
ex = < 1/2
lnex = < ln(1/2)
x= < ln1-ln(2)
x =< -ln2

donc s = -ln2

C'est bien une réponse comme sa ?
Merci

par **Carpate** » 01 Fév 2012, 16:41

[quote="Neijin46"]Bonjour, j'ai un soucis,on me demande de faire ça
g(x) = (ex+1)(2ex-1)
Justifier que g(x) est du signe de 2ex-1. En déduire que g(x)>0 pour x >-ln2 et g (x)0 car une exponentielle est toujours positive et 1>0 donc g(x) est du signe de 2ex-1.
La j'ai justifié que g(x) était du signe de 2ex-1. Ensuite j'en déduis que g(x)>0 pour x >-ln2 et g (x)0 ex+1>0
2ex > 1 ex>-1
ex > 1/2
ln(ex) > ln(1/2) Impossible car une exponentielle est toujours positive
x >ln1-ln(2)
x>-ln2

Donc S=-ln2 ( entre acolade)

2ex-1= 0,

La fonction exponentielle étant monotone croissante sur R, e^x > e{ln(1/2)} est équivalent à
x > ln(1/2) soit x > -ln 2
f(x) négative sur ]-infini ; -ln2[ , positive sur ]-ln2 ; +infini[

par **Neijin46** » 01 Fév 2012, 16:47

Posté par Neijin46
Bonjour, j'ai un soucis,on me demande de faire ça
g(x) = (ex+1)(2ex-1)
Justifier que g(x) est du signe de 2ex-1. En déduire que g(x)>0 pour x >-ln2 et g (x)< ou égale pour x < ou égale a -ln2.
voila ce que j'ai répondu,
Pour tout réel x, ex>0 car une exponentielle est toujours positive et 1>0 donc g(x) est du signe de 2ex-1.
La j'ai justifié que g(x) était du signe de 2ex-1. Ensuite j'en déduis que g(x)>0 pour x >-ln2 et g (x)< ou égale pour x < ou égale a -ln2 avec les inéquations ci-dessous

e^x+1>0
e^x>-1
Impossible car une exponentielle est toujours positive

2ex-1>0
2e^^x > 1
ex > 1/2
ln(ex) > ln(1/2)
x >ln1-ln(2)
x>-ln2

Donc S=-ln2 ( entre acolade)

2e^x-1= <0
2e^x= < 1
e^x = < 1/2
lne^x = < ln(1/2)
x= < ln1-ln(2)
x =< -ln2

donc s = -ln2

J'ai mieux présenter ma réponse.
Bonjour carpate, ce que tu me dit c'est similaire a ma réponse ou je dois modifier des choses?

par **Neijin46** » 01 Fév 2012, 16:50

Définir l'ensemble de définition est-il vraiment utile? Car sur la question on ne me le demande

par **Carpate** » 01 Fév 2012, 16:55

[quote="Neijin46"]Posté par Neijin46
Bonjour, j'ai un soucis,on me demande de faire ça
g(x) = (ex+1)(2ex-1)
Justifier que g(x) est du signe de 2ex-1. En déduire que g(x)>0 pour x >-ln2 et g (x)0 car une exponentielle est toujours positive et 1>0 donc g(x) est du signe de 2ex-1.
Là j'ai justifié que g(x) était du signe de 2ex-1. Ensuite j'en déduis que g(x)>0 pour x >-ln2 et g (x)0
e^x>-1
Impossible car une exponentielle est toujours positive

2ex-1>0
2e^^x > 1
ex > 1/2
ln(ex) > ln(1/2)
x >ln1-ln(2)
x>-ln2

Donc S=-ln2 ( entre acolade)

2e^x-1= 0 car une exponentielle est toujours positive et 1>0 donc g(x) est du signe de 2ex-1.
La j'ai justifié que g(x) était du signe de 2ex-1.[/COLOR]
Oui :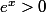

soit

et

mais ça ne justifie pas :

!

par **Carpate** » 01 Fév 2012, 16:58

Neijin46 a écrit:Définir l'ensemble de définition est-il vraiment utile? Car sur la question on ne me le demande

Si tu avais étudié le domaine de définition de g(x) tu n'aurais pas écrit :
"g(x)>0 pour x >-ln2 et g (x)< ou égale pour x < ou égale a -ln2"
g(x) n'est pas défini en x = - ln 2 !

par **Neijin46** » 01 Fév 2012, 17:01

Carpate a écrit:Si tu avais étudié le domaine de définition de g(x) tu n'aurais pas écrit :
"g(x)>0 pour x >-ln2 et g (x)< ou égale pour x < ou égale a -ln2"
g(x) n'est pas défini en x = - ln 2 !

C'est sur la question demandé que ceux-ci est écrit.

par **Carpate** » 01 Fév 2012, 17:04

Neijin46 a écrit:Posté par Neijin46
Bonjour, j'ai un soucis,on me demande de faire ça
g(x) = (ex+1)(2ex-1)
Justifier que g(x) est du signe de 2ex-1. En déduire que g(x)>0 pour x >-ln2 et g (x)0 car une exponentielle est toujours positive et 1>0 donc g(x) est du signe de 2ex-1.
La j'ai justifié que g(x) était du signe de 2ex-1. Ensuite j'en déduis que g(x)>0 pour x >-ln2 et g (x)0
e^x>-1
Impossible car une exponentielle est toujours positive

2ex-1>0
2e^^x > 1
ex > 1/2
ln(ex) > ln(1/2)
x >ln1-ln(2)
x>-ln2

Donc S=-ln2 ( entre acolade)

2e^x-1= <0
2e^x= < 1
e^x = < 1/2
lne^x = < ln(1/2)
x= < ln1-ln(2)
x =< -ln2

donc s = -ln2

J'ai mieux présenter ma réponse.
Bonjour carpate, ce que tu me dit c'est similaire a ma réponse ou je dois modifier des choses?

Le calcul est correct mais ne présente pas le résultat sous la forme S = ...
Ce n'est pas une inéquation à résoudre, on te demande le signe de g(x) selon les valeurs de x.
Ecris : f(x) négative sur ]-infini ; -ln2[ , positive sur ]-ln2 ; +infini[

par **Neijin46** » 01 Fév 2012, 17:12

Carpate a écrit:Le calcul est correct mais ne présente pas le résultat sous la forme S = ...
Ce n'est pas une inéquation à résoudre, on te demande le signe de g(x) selon les valeurs de x.
Ecris : f(x) négative sur ]-infini ; -ln2[ , positive sur ]-ln2 ; +infini[

Oué c'est plus logique avec cette phrase, Donc en faites avec la réponse que j'ai fais, j'ai bien répondu a la question.

Merci beaucoup Carpate

par **Carpate** » 01 Fév 2012, 17:20

Neijin46 a écrit:C'est sur la question demandé que ceux-ci est écrit.

Je persiste et signe.
Il faut supprimer les deux "ou égale" en rouge dans l'énoncé (tel que tu l'as écrit) :
"Justifier que g(x) est du signe de 2ex-1. En déduire que g(x) > 0 pour x > -ln2 et g (x) < 0 ou égale pour x < ou égale a -ln2"
En effet :
a) la fonction g n'existe pas en - ln 2
b) autrement dit g admet une asymptote verticale d'équation y = - ln 2

par **Neijin46** » 01 Fév 2012, 17:26

Carpate a écrit:Je persiste et signe.
Il faut supprimer les deux "ou égale" en rouge dans l'énoncé (tel que tu l'as écrit) :
"Justifier que g(x) est du signe de 2ex-1. En déduire que g(x) > 0 pour x > -ln2 et g (x) < 0 ou égale pour x < ou égale a -ln2"
En effet :
a) la fonction g n'existe pas en - ln 2
b) autrement dit g admet une asymptote verticale d'équation y = - ln 2

C'est bizarre car c'est vraiment ce qu'il y a écrit dans l'énoncé et c'est un extrait de bac de 1997.

C'est pas écrit ou égale mais tu sais c'est une barre en dessous de < qui signifie ou égale

par **Carpate** » 01 Fév 2012, 17:32

Neijin46 a écrit:C'est bizarre car c'est vraiment ce qu'il y a écrit dans l'énoncé et c'est un extrait de bac de 1997.

C'est pas écrit ou égale mais tu sais c'est une barre en dessous de < qui signifie ou égale

En effet.
Tu n'as qu'à en parler à ton prof.

par **geegee** » 01 Fév 2012, 18:41

[quote="Neijin46"]Bonjour, j'ai un soucis,on me demande de faire ça
g(x) = (ex+1)(2ex-1)
Justifier que g(x) est du signe de 2ex-1. En déduire que g(x)>0 pour x >-ln2 et g (x)0 car une exponentielle est toujours positive et 1>0 donc g(x) est du signe de 2ex-1.
La j'ai justifié que g(x) était du signe de 2ex-1. Ensuite j'en déduis que g(x)>0 pour x >-ln2 et g (x)0 ex+1>0
2ex > 1 ex>-1
ex > 1/2
ln(ex) > ln(1/2) Impossible car une exponentielle est toujours positive
x >ln1-ln(2)
x>-ln2

Donc S=-ln2 ( entre acolade)

2ex-1= 0 donc (ex+1)(2ex-1) est du signe de (2ex-1)
g(x)>0 pour x >-ln2
g(x) > 0 2ex-1 > 0 2ex > 1 ex> 1/2 x> -ln2

Exponentielle

Exponentielle

Qui est en ligne