Algèbre linéaire
27 messages
- Page 2 sur 2 - 1, 2
aviondechasse a écrit:Il y a un gros malentendu.
f et p ne désignent pas la même application : p=(f^2+f+id)/7, je l'ai dit plus haut.
Un projecteur, dans mon cours, c'est une application linéaire p vérifiant p^2=p.
oui, ça va je viens de regler tout ça.
C'est ça la défdinition d'un projecteur.
Le cours devrait donner aussi une propriété des projecteur :
Ah mais non je suis bête ce sont des droites vectorielles j'aurais du y réfléchir à deux fois avant de poster...
Au passage merci à MOHAMED_AIT_LH et Joker62 pour leur aide sur mon précédent exercice. :)
Edit : En fait j'ai encore besoin de vous, je ne comprends absolument pas la correction de la question 2b ^^.
Au passage merci à MOHAMED_AIT_LH et Joker62 pour leur aide sur mon précédent exercice. :)
Edit : En fait j'ai encore besoin de vous, je ne comprends absolument pas la correction de la question 2b ^^.
Salut
Je t'en prie.
Je te la détaille un peu :
Soit Alors
Alors  est un vecteur directeur de
est un vecteur directeur de  .Soit
.Soit  l'application de
l'application de  vers
vers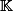 qui associe à chaque vecteur
qui associe à chaque vecteur  l'unique scaliare
l'unique scaliare ) tel que
tel que -x=\phi(x) u.)
 Montrons d'abord que
Montrons d'abord que  est linéaire :
est linéaire :
Soit et
et  \in E^2) , on a
, on a -x=\phi(x) u) et
et  - y = \phi(y) u) donc : Alors :
donc : Alors : + \lambda f(y) - (x+ \lambda y) = \phi(x) u + \lambda \phi(y) u)
Par linéarité de on a alors
on a alors  - (x+y ) =(\phi(x) + \lambda \phi(y))u)
Or, par définition de on a :
on a : -(x+y)= \phi(x+y) u) alors :
alors :  = \phi(x) + \lambda \phi(y)) .Il en résulte que
.Il en résulte que  est une forme linéaire sur
est une forme linéaire sur 
 Si
Si 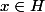 alors
alors =x) , ce qui donne :
, ce qui donne : -x=0 u) , donc
, donc =0) , il en résulte que
, il en résulte que  , par suite :
, par suite :  ou
ou  .
.
Pour conclure que il faut prouver que
il faut prouver que  est non nulle. Or c'est le cas car
est non nulle. Or c'est le cas car  veut dire :
veut dire : -x=0) , ce qui veut dire que
, ce qui veut dire que  , ce qui n'est pas le cas par définition d'une transvection hyperplane (voir la définition dans le fichier pdf).
, ce qui n'est pas le cas par définition d'une transvection hyperplane (voir la définition dans le fichier pdf).
Effectivement, la solution donnée dans le pdf n'a pas bien expliqué pourquoi le rang de est égal à
est égal à  : c'est justement parce que
: c'est justement parce que  et que
et que 
aviondechasse a écrit:Au passage merci à MOHAMED_AIT_LH et Joker62 pour leur aide sur mon précédent exercice.
Je t'en prie.
aviondechasse a écrit:En fait j'ai encore besoin de vous, je ne comprends absolument pas la correction de la question 2b ^^.
Je te la détaille un peu :
Soit
Soit
Par linéarité de
Or, par définition de
Pour conclure que
Effectivement, la solution donnée dans le pdf n'a pas bien expliqué pourquoi le rang de
27 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 231 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
