Algèbre linéaire
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 21 Jan 2012, 22:33
par Joker62 » 21 Jan 2012, 22:33
Hello !
A quoi correspond f^3, f^2 selon toi ?
Pour la dernière question : on a une relation entre f^3 et des puissances successives de f.
Envoie toutes ces puissances d'un côté en laissant le Id de l'autre et applique f^-1 ;)
-
aviondechasse
- Membre Naturel
- Messages: 13
- Enregistré le: 21 Jan 2012, 19:22
-
 par aviondechasse » 21 Jan 2012, 23:24
par aviondechasse » 21 Jan 2012, 23:24
Les exposants au sens
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 22 Jan 2012, 01:13
par Joker62 » 22 Jan 2012, 01:13
Que peux-tu dire de la somme ker(p) + Im(p) ?
Peux-tu en déduire la dimension de Im(p) ?
-
aviondechasse
- Membre Naturel
- Messages: 13
- Enregistré le: 21 Jan 2012, 19:22
-
 par aviondechasse » 22 Jan 2012, 01:43
par aviondechasse » 22 Jan 2012, 01:43
Effectivement on peut raisonner en terme de dimension avec le théorème du rang, mais dans la mesure ou on me demande de préciser les ensembles ker f et im f, autant y aller directement par le calcul non ?

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 22 Jan 2012, 04:35
par alm » 22 Jan 2012, 04:35
Salut,
L'esprit de la question voudrait plutôt diriger vers l'idée que comme

, on a :
\circ f =\text{Id})
et de conclure en posant
)
que

Effectivement, le fait de demander de prouver que

est bijective est une répétition, mais le fait de calculer son inverse n'es est pas une , et on voit bien l'expression de

à travers cette question.
-
aviondechasse
- Membre Naturel
- Messages: 13
- Enregistré le: 21 Jan 2012, 19:22
-
 par aviondechasse » 22 Jan 2012, 13:39
par aviondechasse » 22 Jan 2012, 13:39
Merci de cette précision.
Est-il possible aussi de me donner l'expression explicite de Im p pour que je puisse comparer ?
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 22 Jan 2012, 14:22
par Joker62 » 22 Jan 2012, 14:22
Re.
Si ker(p) et Im(p) sont en somme directe et que tu connais parfaitement Ker(p).
Il suffit de trouver un vecteur qui n'est pas dans le noyau pour qu'il soit dans l'image.
Et comme Im(p) est forcément de dimension 1, tu as le sev entier en prenant le vect.
-
aviondechasse
- Membre Naturel
- Messages: 13
- Enregistré le: 21 Jan 2012, 19:22
-
 par aviondechasse » 22 Jan 2012, 15:04
par aviondechasse » 22 Jan 2012, 15:04
Salut,
Je ne suis pas
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 22 Jan 2012, 15:30
par Joker62 » 22 Jan 2012, 15:30
Excuse moi !
J'ai dit une bêtise !
Chaque vecteur de R^3 se décompose de manière unique comme la somme d'un vecteur de ton plan et d'un vecteur de ta droite vectorielle !
En fait, si tu prends un vecteur normal à ton plan, ça devrait suffire.
(1;1;1) par exemple !

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 22 Jan 2012, 16:22
par alm » 22 Jan 2012, 16:22
Salut ,
Joker62 a écrit:Re.
Si ker(p) et Im(p) sont en somme directe et que tu connais parfaitement Ker(p).
Il suffit de trouver un vecteur qui n'est pas dans le noyau pour qu'il soit dans l'image.
Et comme Im(p) est forcément de dimension 1, tu as le sev entier en prenant le vect.
Attention ! ceci n'est pas vrai !
Je m'explique :
Si

est un endomorphisme de

tel que
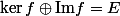
alors l'image de

est un supplémentaire de
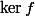
, mais la réciproque n'est pas juste (sionon par exemple l'image prendra une infinité de "valeurs" à savoir tous les sous-espaces supplémentaires à
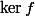
.

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 22 Jan 2012, 16:24
par alm » 22 Jan 2012, 16:24
Salut
Joker62 a écrit:En fait, si tu prends un vecteur normal à ton plan, ça devrait suffire.
(1;1;1) par exemple !
On ne peut pas parler à présent de vecteur normal, car on a juste une structure d'espace vectoriel
Pour en parler il faut avoir un produit scaliare donc un espace euclidien (ou préhilbertien généralement)
-
aviondechasse
- Membre Naturel
- Messages: 13
- Enregistré le: 21 Jan 2012, 19:22
-
 par aviondechasse » 22 Jan 2012, 16:28
par aviondechasse » 22 Jan 2012, 16:28
Euh on n'a pas encore fait les produits scalaires et tout ca dont je crois pas que je puisse parler de vecteur normal.
Edit : grillé :)
-
Joker62
- Membre Transcendant
- Messages: 5027
- Enregistré le: 24 Déc 2006, 19:29
-
 par Joker62 » 22 Jan 2012, 16:29
par Joker62 » 22 Jan 2012, 16:29
Oui évidemment.
On est dans R^3 malgré tout.
On peut en parler implicitement.
-
aviondechasse
- Membre Naturel
- Messages: 13
- Enregistré le: 21 Jan 2012, 19:22
-
 par aviondechasse » 22 Jan 2012, 16:32
par aviondechasse » 22 Jan 2012, 16:32
Comment faire alors ?

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 22 Jan 2012, 16:36
par alm » 22 Jan 2012, 16:36
aviondechasse a écrit:Merci de cette précision.
Est-il possible aussi de me donner l'expression explicite de Im p pour que je puisse comparer ?
Elle devant toi d'après la définition de

Préxisément tu as :
 / (x,y,z) \in {\mathbb R}^3\} \\ &=& \{(x+y+2z,x,y) / (x,y,z) \in {\mathbb R}^3 \} \\ &=& \{x(1,1,0) + y(1,0,1) + z(2,0,0) / (x,y,z) \in {\mathbb R}^3 \} \\&=& \text{Vect} \{(1,1,0),(1,0,1),(2,0,0) \}\\&=& \text{Vect} \{(1,1,0),(1,0,1),(2,0,0) \} \end{eqnarray})
Il est facil ensuite de prouver que la famille
,(1,0,1),(1,0,0) ))
est libre pour mener à bien tes verifications .
Edit : c'est une réponse pour f et pas pour p
-
aviondechasse
- Membre Naturel
- Messages: 13
- Enregistré le: 21 Jan 2012, 19:22
-
 par aviondechasse » 22 Jan 2012, 16:52
par aviondechasse » 22 Jan 2012, 16:52
2). Faute de frappe ?

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 22 Jan 2012, 16:56
par alm » 22 Jan 2012, 16:56
Je suis d'accord que dans
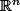
en général on peut parler de la structure euclidienne canonique et de vecteur normal dans cette structure

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 22 Jan 2012, 17:00
par alm » 22 Jan 2012, 17:00
aviondechasse a écrit:Edit : En fait je ne comprends pas pourquoi ton (2,0,0) s'est transformé en (0,0,2). Faute de frappe ?
c'est une erreur de vitesse , c'est réctifié c'est bien (2,0,0)

-
alm
- Membre Relatif
- Messages: 335
- Enregistré le: 15 Jan 2009, 01:00
- Localisation: Salé, Maroc
-
 par alm » 22 Jan 2012, 17:03
par alm » 22 Jan 2012, 17:03
Salut
Je suis vraiment désolé car je viens de découvrir que l'exo a une suite dans laquelle on a définit p=u/7 ...
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 27 invités
 , on a :
, on a : \circ f =\text{Id}) et de conclure en posant
et de conclure en posant ) que
que 
 est bijective est une répétition, mais le fait de calculer son inverse n'es est pas une , et on voit bien l'expression de
est bijective est une répétition, mais le fait de calculer son inverse n'es est pas une , et on voit bien l'expression de  à travers cette question.
à travers cette question. est un endomorphisme de
est un endomorphisme de  tel que
tel que 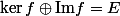 alors l'image de
alors l'image de  est un supplémentaire de
est un supplémentaire de 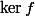 , mais la réciproque n'est pas juste (sionon par exemple l'image prendra une infinité de "valeurs" à savoir tous les sous-espaces supplémentaires à
, mais la réciproque n'est pas juste (sionon par exemple l'image prendra une infinité de "valeurs" à savoir tous les sous-espaces supplémentaires à 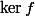 .
.