Exercice sur les suites terminale

[cmm1]

Bonjour, pourriez vous m'aider pour cet exo s'il vous plait.

A l'aide du calcul des premiers termes, conjecturer le sens de variation de la suite (un) . Valider ou invalider
ensuite votre conjecture par une démonstration.
1) (un) est la suite définie pour tout entier naturel n par un = n^3 – 2 n² – n
2) (un) est la suite définie pour tout entier naturel n>0 par un = (n/2) + (8/n)
3) ( un) est la suite définie pour tout entier naturel n par un =
(30n)/(25+n²)
4) ( un) est la suite définie pour tout entier naturel n par un = 2n+sin (n) .

Ensuite, pour chaque suite: est elle minorée ? majorée ? bornée ?

Pour l'instant voici ce que j'ai fait : (je ne détail pas tous les calculs )
I)
1) u0 = 0 ; u1 = -2 ; u2 = -2 ; u3 = 6
Conjecture : suite croissante pour n>= 1
Démonstration :
u(n+1) - un = 3n² - n - 2
Or on a
- n² >= n d'ou n² - n >= 0
- 2n² >= 2 d'ou n² - 2 >= 0
Par sommation: 3n² - n - 2 >= 0 d'ou validation de la conjecture.

2) u1 environ 8.5 ; u2 environ 5 ; u3 environ 4.2
Conjecture : suite strictement décroissante
Démonstration :
u(n+1) - un = (n² + n - 16) / [2n(n+1)]
ICI JE BLOQUE

3) u0 = 0 ; u1 environ 1.15 ; u2 environ 2.07 ; u3 environ 2.65
Conjecture ???
Démonstration :
U(n+1) - un = (-60n² + 60n + 30) / [25+(n+1)²]
ICI JE BLOQUE AUSSI

C'est tout ce que j'ai fait pour le moment
Merci d'avance !!!

[SaintAmand]

Bonjour,

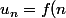2) u1 environ 8.5 ; u2 environ 5 ; u3 environ 4.2
Conjecture : suite strictement décroissante
Démonstration :
u(n+1) - un = (n² + n - 16) / [2n(n+1)]

Factorise le numérateur.

3) u0 = 0 ; u1 environ 1.15 ; u2 environ 2.07 ; u3 environ 2.65
Conjecture ???
Démonstration :
U(n+1) - un = (-60n² + 60n + 30) / [25+(n+1)²]

Pareil.

Tu pouvais aussi remarquer que les suites sont de la forme .