Doraki a écrit:non on te demande pas de trouver des générateurs qui commutent avec tout le monde.
Il faut trouver une famille de générateurs qui commutent entre eux (et pas qui commutent avec entre eux et aussi avec ceux qu'on a pas pris)
Merci de ton aide. Mais j'ai trouvé ma réponse dans "Introduction to Mathematical Physics" M.T. Vaughn page 468:
[HTML]The rank of semisimple Lie Algebra A is the maximum number of linearly independent commuting elements of the algebra.
The rank of the Lie algebra SU(2) is one;
any of the
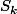
(
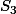
, say) commutes with itself,
but then

and

do not commute with
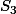
.
The rank of the Lie algebra SU(3) is two since

and

commute, but no independent element commutes with both of these.
In general, the rank of the Lie algebra of SU(n) is n-1
[/HTML]
Ici les S_k sont les matrices de Pauli, I_k décrit plus haut.
Donc on a bien le droit de compter le generateur qui commute avec lui meme. Je crois que ce qu'a dit Doraki est equivalent, mais je ne suis pas sur. Désolé j'ai un peu du mal, ca fait plus de dix ans que j'ai pas fait d'algebre

Merci et probablement à bientot pour d'autres questions sur le sujet!
