Les suites 2.
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Grigori
- Membre Naturel
- Messages: 17
- Enregistré le: 18 Nov 2011, 22:03
-
 par Grigori » 19 Nov 2011, 18:07
par Grigori » 19 Nov 2011, 18:07
Salut.
Soit
)
une suite décroissante et :
)
: 0 <

1) Prouver que quelque soit p et q de IN tels que p < q on a :

2) Prouver que quelque soit p et q de IN tels que p < q on a :

Votre aide s'il vous plaît et merci infiniment!
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 19 Nov 2011, 18:48
par el niala » 19 Nov 2011, 18:48
1) tu n'as rien trouvé ?

c'est immédiat non ?
et comme
 \ \gt \alpha_p -\alpha_q)
...
-
Grigori
- Membre Naturel
- Messages: 17
- Enregistré le: 18 Nov 2011, 22:03
-
 par Grigori » 19 Nov 2011, 18:52
par Grigori » 19 Nov 2011, 18:52
el niala a écrit:1) tu n'as rien trouvé ?

c'est immédiat non ?
et comme
 \ \gt \alpha_p -\alpha_q)
...
Merci beaucoup!
Et la deuxiéme ?
Merci!
-
el niala
- Membre Irrationnel
- Messages: 1014
- Enregistré le: 07 Nov 2011, 20:26
-
 par el niala » 19 Nov 2011, 19:20
par el niala » 19 Nov 2011, 19:20
la deuxième, c'est un peu plus cher, tu pourrais essayer de chercher un peu non ?
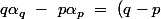\alpha_q\ \ +\ p(\alpha_q - \alpha_p))
essaie de terminer, ce n'est pas bien compliqué
-
Grigori
- Membre Naturel
- Messages: 17
- Enregistré le: 18 Nov 2011, 22:03
-
 par Grigori » 19 Nov 2011, 20:11
par Grigori » 19 Nov 2011, 20:11
el niala a écrit:la deuxième, c'est un peu plus cher, tu pourrais essayer de chercher un peu non ?
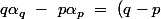\alpha_q\ \ +\ p(\alpha_q - \alpha_p))
essaie de terminer, ce n'est pas bien compliqué
Je cherche toujours avant de poster l'exercice.
-
Grigori
- Membre Naturel
- Messages: 17
- Enregistré le: 18 Nov 2011, 22:03
-
 par Grigori » 20 Nov 2011, 10:47
par Grigori » 20 Nov 2011, 10:47
el niala a écrit:la deuxième, c'est un peu plus cher, tu pourrais essayer de chercher un peu non ?
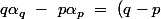\alpha_q\ \ +\ p(\alpha_q - \alpha_p))
essaie de terminer, ce n'est pas bien compliqué
Merci beaucoup pour votre aide, je l'ai trouvé. :ptdr:
Merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités