Les suites.

[Grigori]

Salut.

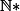
1) a ) Prouver que quelque soit n de l'équation : admet une solutions unique dans l'interval ]0;1[.

1) b) Comparez et .

1) c) Prouver que : :

1) d) Prouver que : est convergente et calculez

________________

1) a) Théorème des valeurs intermédiares.

1) b) Votre aide s'il vous plaît!

1) c) Votre aide s'il vous plaît!

1) d) Votre aide s'il vous plaît!

Merci infiniment!

[el niala]

1b) tu connais non ? et comme et

1c) pense au sens de variation des 2 fonctions

1d) suite croissante majorée...

[Grigori]

1b) tu connais non ? et comme et

1c) pense au sens de variation des 2 fonctions

1d) suite croissante majorée...

________________

Merci d'abord pour votre aide.

1) b) > 1

et

donc on a :

Et puisque la fonction décroissente on a :

1) c) On a : :

Votre aide s'il vous plaît!
Merci beaucoup.

[el niala]

1b) [FONT=Comic Sans MS]arnaque[/FONT] va écrire en marge le correcteur, car tu ne démontres pas ton résultat

et comme la fonction arcosinus est décroissante...

1c) je ne comprends pas ta démarche
raisonne par l'absurde,


suppose
compare :



1d) tu connais un majorant à cette suite non ?

et conclus

[Grigori]

1b) [FONT=Comic Sans MS]arnaque[/FONT] va écrire en marge le correcteur, car tu ne démontres pas ton résultat

et comme la fonction arcosinus est décroissante...

1c) je ne comprends pas ta démarche
raisonne par l'absurde,


suppose
compare :



1d) tu connais un majorant à cette suite non ?

et conclus

Ah ça y est!
Merci beaucoup pour votre aide!