Existence d'un valeur particulière de f'

[skeer3034]

Bonjour,
(Mon premier message sur ce forum, je me présente en quelques mots: étudiant en classe préparatoire (PSI) , en 5/2)
Je me permets de vous écrire car j'ai eu une question en colle, à laquelle, même après avoir bien réfléchi, je ne trouve pas de solution:

f dérivable de [a;b] dans R , on a f'(a)=f'(b)=0
Je voudrai montrer qu'il existe c appartenant à [a;b] tel que f'(c)=( f(c) - f(a) ) / ( c - a )

Je voudrai donc prouver que la fonction f'(x)- (f(x)-f(a))/(x-a) s'annule sur l'intervalle mais je n'y arrive pas?

Si vous pouviez m'aider?

En vous remerciant par avance.

[Le_chat]

Salut, si tu dis que g(x)=(f(x)-f(a))/(x-a), que dire d'un extrema de g?

Ca devrait t'aider à avancer.

Si tu veux, pour trouver la bonne fonction à considérer, il faut toujours dans ce genre d'exo, faire un dessin: tu traces une courbe sur ton intervalle, plate en a et b, et tu essayes de trouver les points candidats. Ici, on se rend compte que ce sont ceux où la courbe vient toucher la pente, on voit bien que c'est un extrema de la pente.

[skeer3034]

Merci pour ces conseils, j'avais fait le petit dessin, et m'étais rendu compte que ce changement de concavité de la courbe convenait.
Malheureusement j'ai du mal à poursuivre.
Un maximum de g est atteind en un point ou la droite reliant le point a et ledit point a une pente maximale mais qu'en tirer?
Je n'arrive pas à en conclure que f'(x)- (f(x)-f(a))/(x-a) s'annule en ce point...!

Dans tout les cas, merci pour cette réponse.
Au plaisir de vous lire.

[Le_chat]

Tu peux calculer la dérivée de g!

[skeer3034]

En effet, je vois que je tourne autour:
Quand je calcule g' j'ai une fonction qui ressemble beaucoup à celle dont je veux prouver qu'elle s'annule en c.
Mais ..... je pourrai conclure si jamais je savais que le fonction g admet un maximum en c (autrement qu'en disant, "je le vois sur le dessin") j'aurai alors: g atteins un maximum en un point intérieur à l'intervalle [a;b] donc sa dérivée s'annule en c et j'aurai ainsi finis.
Mais malheureusement je ne vois pas comment expliquer que g atteins un max en c (le point de changement de concavité).

je réfléchis...... pourquoi existe t-il forcément un max de g intérieur à [a;b]? pour que ce ne soit pas le cas il faudrait que f possède un sens de variation strict or ce n'est pas le cas puisque f'(a)=f'(b)=0 .
C'est un peu fait "avec les mains" mais je pense que c'est ça, qu'en pensez vous?

[mathelot]

c'est un point de la courbe C(f) d'abscisse
qui admet une tangente passant par


ici


je pense pas que ça soit un extremum de f '
pour un contre-exemple, faire les calculs avec




en

[mathelot]

1er cas

supposons f ' continue sur [a,b]
alors f' est bornée sur [a,b] et atteint son min en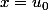 et son max en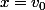

la fonction



est continue sur [a,b], négative en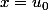 , positive en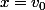
d'après le théorème des accroissements finis.





elle s'annule en
d'après le théorème des valeurs intermédiaires

2ème cas

malheureusement
montre que f peut être dérivable sur le compact [0;1] sans que f' ne soit bornée ni continue....
il faut trouver un argument plus sophistiqué que ma démo qui suppose f de classe

je crois qu'il y a un théorème d'analyse assez fin (théorème de L3, cher Nightmare ? :we: )
qui dit que si h est une dérivée , elle vérifie alors le théorème des valeurs intermédiaires,
même si n'est pas continue ..
le souci , c'est que cet argument élève nettement le niveau mathématique de la réponse

[mathelot]

finalement la démo se trivialise

soit

<--- FAUX g(b) =0

g est continue sur le fermé [a,b] , dérivable sur ]a,b[
d'après Rolle il existe tq
avec


c'est donc bien un extremum de g

[skeer3034]

Il ne me semble pas que nous ayons g(b)=0.

En vous remerciant pour l'attention que vous portez à ma question.

[Le_chat]

Alors en fait c'est un peu délicat:

Si g' s'annule sur ]a,b[, c'est bon, et on va montrer que c'est toujours le cas.

On a g(a)=0, g(b)=(f(b)-f(a))/(b-a).

A cause de fonctions très bizarre, je n'ai rien trouvé de plus joli qu'un raisonnement par l'absurde, mais on doit surement pouvoir s'en passer: Si g' ne s'annule pas sur ]a,b[, alors g est strictement monotone.

On suppose par exemple g croissante:
on a alors pour tout x de ]a,b[, par hypothèse, 0
Avec un bon dessin, on se rend compte que ça va merder au voisinage de b: il semble que g(x) soit plus grand que g(b) près de b.

On dit alors que au voisinage de b,g(x)-g(b) est équivalent à(x-b)g'(b)=(b-x)(f(b)-f(a))/(x-a)^2 ce qui est positif au voisinage de b! Donc, pour x assez proche de b, g(x)-g(b)>0, on a notre absurdité!



Si g est décroissante, c'est la même chose, g(x)-g(b) est équivalent à(x-b)g'(b)=(b-x)(f(b)-f(a))/(x-a)^2 ce qui ici sera négatif (car dans ce cas, f(b)

[mathelot]

Si g' ne s'annule pas sur ]a,b[, alors g est strictement monotone.

ça c'est vrai , mais c'est c'est un argument non trivial. Pourquoi ?
lorsque une fonction k=g' est une dérivée , elle vérifie le théorème
des valeurs intermédiaires même si elle n'est pas continue, et donc que si g' changeait de signe, effectivement, g' s'annulerait, mais pas parce que g' est nécessairement continue mais parce que c'est une dérivée (on utilise un argument au moins de niveau Bac+3 ici ?)

[Le_chat]

Hum... Si g' ne s'annule pas, alors g'>0 ou g'<0 ( car elle verifie le TVI, comme tu l as si bien fait remarquer, c'est le théorème de Darboux)


La preuve est de niveau L2, il faut un peu de topologie pour le faire rapidement (on peut même le faire avec les simples outils d'analyse de première année). Comme skeer3034 fait 5/2, il a surement les outils pour le démontrer, et il l'a peut être même déjà fait l'année dernière.

Pour une preuve, voir sur wikipedia :lol3:

[skeer3034]

(bon dsl ça fait up le topic)
C'était juste pour remercier les deux membres qui ont répondu à ma question!
Merci à vous deux.