Exercice - Fonction/extremum ...

[tick56]

Bonjour, voilà je n'arrive pas à faire cette exercice :$ Pouvez me donnez des réponses et m'expliquer ?

:::::


Soit f la fonction définie pour tout réel x par f (x) = 9-4x² / x² + 1 .


On note Cf sa courbe représentative dans le plan muni d'un repère.

1. Calculer les coordonnées des points d'intersection de la courbe Cf avec les axes du repère.

2. Etudier le signe de f(x) - f(0). En déduire l'existence d'un extremum pour la fonction f .

3. Montrer que pour tout réel x, f(x) > -4 . peut on conclure que -4 est le minimum de la fonction f ?

[XENSECP]

Je suppose que la 1) t'as pas posé trop de problème ?

[tick56]

1) Faut faire :
9-4x²/x²+1=0 (x;0)
f(0) ---> (0;x)

??


9-4x² = 0
3²-2x² = 0
(3+2x)(3-2x)= 0
9-6x+6x-4x = 0
9-4x = 0
-4x=-9
x= -9/-4
x=2.25

ou

x²-1=0
x²=1
x=1

et

f(0) = 9

donc les points d'intersection : (0;9) ; (2.25;0) ; (1;0)

???? J'ai jamais compris ça, est-ce que c'est bon sinon corrige moi ;)

[tick56]

A quoi que, si on fait l'équation , si on la résolue il reste que 9-4x² et donc il faut calculer juste 9-4x²=0 pour trouver les coordonnéeS [avec f(0)]?

[tick56]

Ou 9-4 ?

Je sais pas trop ! Aidez-moi j'ai besoin que l'on m'éclaire là-dessus ^^'

[XENSECP]

Le principe est bon. La résolution bof

[tick56]

Tu peux m'aider ?? :)

[XENSECP]

Repartons de ce qui est bon :

1) Faut faire :
9-4x²/x²+1=0 (x;0)
f(0) ---> (0;x)

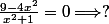
[tick56]

9-4x²/x²+1 = 0
(après avoir fait le calcul 9-4x²/x²+11):

9-4 = 0
9-4 = x
x = 5

??

[XENSECP]

Tu as quelle équation à résoudre à partir de ce que j'ai écrit ?

[tick56]

9-4x²/x²+1 = 0 ?


x²+1 = -9+4x²
x+1 = -9+4x
x = -1 -9 +4x
x = -10 + 4x

0 = -6


:cry: Aide - moi ! :$ Je suis perdu ^^'
Surtout que les 2 questions suivantes sont plus dûr ....

[tick56]

= 9-4x² = 0
a²-b² = (a-b)(a+b) idd.remarquable
= 3² - (2x)² = 0
= (3 - 2x)(3+ 2x) = 0

Soit : 3x-2 = 0 -> x = 3/2
ou 3x+2x= 0 -> x= -3/2
Comme ça?

[XENSECP]

= 9-4x² = 0
a²-b² = (a-b)(a+b) idd.remarquable
= 3² - (2x)² = 0
= (3 - 2x)(3+ 2x) = 0

Soit : 3x-2 = 0 -> x = 3/2
ou 3x+2x= 0 -> x= -3/2
Comme ça?

ça c'est déjà mieux oui

[tick56]

C'est bon?

[tick56]

Tu peux me dire ce que tu trouve Stp comme là je devrais faire le 2) et le 3) :$
Merci d'avance !

[tick56]

Merci d'avance !