Suite Ts
57 messages
- Page 2 sur 3 - 1, 2, 3
On parle de la question 1, il s'agit de démontrer par récurrence que U est décroissante, c'est-à-dire que pour tout n U(n+1) <= Un.
On a déjà que U1 <= U0 (initialisation de la récurrence). Maintenant, si je suppose que U(n+1) <= Un pour un certain n donné, je veux montrer que U(n+2) <= U(n+1). Et pour ça il faut utiliser f.
Pour la question 2 ce sera le même principe, sauf que ce qu'on voudra montrer c'est Un >= 0 pour tout n.
On a déjà que U1 <= U0 (initialisation de la récurrence). Maintenant, si je suppose que U(n+1) <= Un pour un certain n donné, je veux montrer que U(n+2) <= U(n+1). Et pour ça il faut utiliser f.
Pour la question 2 ce sera le même principe, sauf que ce qu'on voudra montrer c'est Un >= 0 pour tout n.
Non. f(x) >= 0 pour tout x ça veut dire que f est positive. Rien à voir avec son sens de variation. J'ai l'impression que tu balances des trucs au hasard sans réfléchir, tu n'arriveras à rien comme ça.
"Quand x croît, f(x) croît aussi" c'est correct, mais pas très précis comme l'a dit Jota Be. Si x <= y et que f est croissante, que dire de f(x) par rapport à f(y) ? Même question pour f décroissante.
"Quand x croît, f(x) croît aussi" c'est correct, mais pas très précis comme l'a dit Jota Be. Si x <= y et que f est croissante, que dire de f(x) par rapport à f(y) ? Même question pour f décroissante.
Skullkid a écrit:Non. f(x) >= 0 pour tout x ça veut dire que f est positive. Rien à voir avec son sens de variation. J'ai l'impression que tu balances des trucs au hasard sans réfléchir, tu n'arriveras à rien comme ça.
"Quand x croît, f(x) croît aussi" c'est correct, mais pas très précis comme l'a dit Jota Be. Si x <= y et que f est croissante, que dire de f(x) par rapport à f(y) ? Même question pour f décroissante.
f(x) <= f(y)?
Essaye de faire des phrases, c'est désagréable de voir pour seule réponse un résultat avec un point d'interrogation à la fin... surtout quand on a posé plusieurs questions.
Oui, la définition de "f est croissante" c'est "pour tous x, y dans le domaine de définition de f, x <= y implique f(x) <= f(y)". Donc tu as tous les outils pour finir ta démonstration.
Oui, la définition de "f est croissante" c'est "pour tous x, y dans le domaine de définition de f, x <= y implique f(x) <= f(y)". Donc tu as tous les outils pour finir ta démonstration.
C'est très confus. Là je lis que tu pars de U(n+2) <= U(n+1) alors que c'est ce que tu prétends démontrer. Et puis tu écris que f est décroissante, c'est faux. Et comme tu raisonnes à l'envers, ça devient incompréhensible...
Une bonne rédaction en maths c'est avant tout une bonne rédaction en français. Ça doit être organisé, on doit voir un début et une fin.
Le début c'est "on suppose que U(n+1) <= Un", et la fin ça doit être "donc U(n+2) <= U(n+1)". Essaye de rédiger la démo complète (y compris l'initialisation) de la décroissance de U, et montre-moi le résultat.
Une bonne rédaction en maths c'est avant tout une bonne rédaction en français. Ça doit être organisé, on doit voir un début et une fin.
Le début c'est "on suppose que U(n+1) <= Un", et la fin ça doit être "donc U(n+2) <= U(n+1)". Essaye de rédiger la démo complète (y compris l'initialisation) de la décroissance de U, et montre-moi le résultat.
Non, ça va toujours pas pour l'hérédité...
Ça n'a aucun sens de dire "on note U(n+1) = f(Un)". U(n+1) est par définition égal à f(Un), tu n'as pas à choisir de le noter comme ça, cette notation t'est imposée. Ensuite tu dis que f(Un) = 1/2 x + 1, mais tu n'as jamais introduit x. De plus tu dis que f(Un) est positif, mais tu ne t'en sers pas (peut-être parce que ça ne sert à rien ici), et tu finis en balançant une conclusion sortie de nulle part...
Une bonne rédaction possible pour l'hérédité est :
On suppose qu'il existe un entier n donné tel que U(n+1) <= Un. Comme f est croissante, cette inégalité implique que f(U(n+1)) <= f(Un), c'est-à-dire U(n+2) <= U(n+1).
C'est tout, y a rien à dire de plus.
Ça n'a aucun sens de dire "on note U(n+1) = f(Un)". U(n+1) est par définition égal à f(Un), tu n'as pas à choisir de le noter comme ça, cette notation t'est imposée. Ensuite tu dis que f(Un) = 1/2 x + 1, mais tu n'as jamais introduit x. De plus tu dis que f(Un) est positif, mais tu ne t'en sers pas (peut-être parce que ça ne sert à rien ici), et tu finis en balançant une conclusion sortie de nulle part...
Une bonne rédaction possible pour l'hérédité est :
On suppose qu'il existe un entier n donné tel que U(n+1) <= Un. Comme f est croissante, cette inégalité implique que f(U(n+1)) <= f(Un), c'est-à-dire U(n+2) <= U(n+1).
C'est tout, y a rien à dire de plus.
BonjourBadMen a écrit:Bonjour, j'ai un exercice à faire sur les suites , et je sais pas quelle méthode appliquer le voici :
On a U0 = 10 et Un+1 = (1/2)Un +1
1) Démontrer que la suite u est décroissante
2)-minorée par 0
3)Déterminer sa limite
Voici les "réflexes mathématiques" à avoir quand on travaille sur une suite récurrente de ce type :
1) SI la suite (Un) converge vers un nombre
2) Comme U0=10 et que L=2 : la suite (Un) doit être décroissante ( à démontrer )
3) Comme U0 >=0 et que Un+1 = (1/2)Un +1 , il semble évident que cette suite est une suite de nombres positifs et donc qu'elle est minorée par 0
@Skullkid
Non ce n'est qu'une indication d'un raisonnement qui est en général correct (et très utile pour certains lycéens)
Bien sûr il EXISTE des exceptions (mais qui sont TRES RARES au niveau du "lycée")
J'aurais du préciser que ce n'est pas une règle "GENERALISABLE" ou VRAI à 100% !!
mais par contre c'est une règle qui peut être appliquée les yeux fermés à 99% des exercices posés au BAC.
En effet il existe des suites qui sont croissantes entre et
et 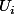 puis décroissante à partir de
puis décroissante à partir de 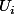 (ou le contraire)
(ou le contraire)
En général on finit par conclure que cette suite est décroissante à partir de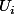 (en fait on finit par ignorer dans l'étude de cette suite les
(en fait on finit par ignorer dans l'étude de cette suite les  premiers termes)
premiers termes)
EDIT(MAJ)
Quand j'ai rédigé mon message précédent j'ai écrit
2) Comme U0=10 et que L=2 : la suite (Un) doit être décroissante ( à démontrer )
Peut être j'aurais du dire : à 99% des cas la suite est décroissante ( IL FAUT LE démontrer )
Non ce n'est qu'une indication d'un raisonnement qui est en général correct (et très utile pour certains lycéens)
Bien sûr il EXISTE des exceptions (mais qui sont TRES RARES au niveau du "lycée")
J'aurais du préciser que ce n'est pas une règle "GENERALISABLE" ou VRAI à 100% !!
mais par contre c'est une règle qui peut être appliquée les yeux fermés à 99% des exercices posés au BAC.
En effet il existe des suites qui sont croissantes entre
En général on finit par conclure que cette suite est décroissante à partir de
EDIT(MAJ)
Quand j'ai rédigé mon message précédent j'ai écrit
2) Comme U0=10 et que L=2 : la suite (Un) doit être décroissante ( à démontrer )
Peut être j'aurais du dire : à 99% des cas la suite est décroissante ( IL FAUT LE démontrer )
1)
Un+1 = (1/2)Un + 1
Si U(n) > 2, alors U(n+1) > (1/2)*2 + 1
Si U(n) > 2, alors U(n+1) > 2
Comme U(0) > 2, alors tous les Un sont > 2 (la suite est minorée par 2)
U(n+1) - Un = (1/2)Un +1 - Un
U(n+1) - Un = 1 - (1/2).Un
Et comme Un > 2, alors --> U(n+1) - Un < 1 - (1/2)*2
U(n+1) - Un < 0 et donc la suite U est décroissante.
La suite Un est décroissante et minorée, elle est donc ...
Un+1 = (1/2)Un + 1
Si U(n) > 2, alors U(n+1) > (1/2)*2 + 1
Si U(n) > 2, alors U(n+1) > 2
Comme U(0) > 2, alors tous les Un sont > 2 (la suite est minorée par 2)
U(n+1) - Un = (1/2)Un +1 - Un
U(n+1) - Un = 1 - (1/2).Un
Et comme Un > 2, alors --> U(n+1) - Un < 1 - (1/2)*2
U(n+1) - Un < 0 et donc la suite U est décroissante.
La suite Un est décroissante et minorée, elle est donc ...
schulhof_2 a écrit:En effet il existe des suites qui sont croissantes entreet
puis décroissante à partir de
(ou le contraire)
En général on finit par conclure que cette suite est décroissante à partir de(en fait on finit par ignorer dans l'étude de cette suite les
premiers termes)
La suite que j'ai donnée est tout à fait niveau lycée, c'est une suite U(n+1) = f(Un) avec f une fonction affine, et elle n'est pas monotone à partir d'un certain rang, elle oscille autour de 2. Je ne pense pas que donner des astuces erronées soit bénéfique, c'est ce genre de "règles" au domaine d'application flou qui parasitent l'intuition d'énormément d'élèves, que ce soit dans le supérieur ou au lycée, à tel point qu'ils n'arrivent parfois pas à s'imaginer qu'une fonction puisse ne pas être monotone/continue/dérivable (de la même façon que tu t'imagines plein de trucs complètement faux quand tu postes sur un sujet qui dépasse tes compétences).
57 messages
- Page 2 sur 3 - 1, 2, 3
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 113 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
