Intégrale et primitif
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
salvinette
- Messages: 7
- Enregistré le: 12 Jan 2011, 20:39
-
 par salvinette » 12 Jan 2011, 20:48
par salvinette » 12 Jan 2011, 20:48
Bonsoir,
j'ai beaucoup de difficultés avec un exercice. Pouvez-vous m'aider ou m'indiquer la marche a suivre pour le résoudre !!!!
Énoncé :
A= lintégrale entre PY/3 et 0 de Cos²
B= l'intégrale entre Py/3 et 0 de Sin²
1°) montrer que A+B = PY/3
2°) montrer que A lintégrale B = Racine carré de 3 / 4
en intégrant par parties
3°) en déduire A et B*
merci a tous
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 12 Jan 2011, 20:55
par Arnaud-29-31 » 12 Jan 2011, 20:55
Salut,
Je suppose que tu voulais dire intégrale entre 0 et
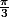
et non pas entre
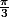
et 0 ...
Tu as écris quoi pour la question 1) ? Celle la doit pas poser de problème en principe.
-
salvinette
- Messages: 7
- Enregistré le: 12 Jan 2011, 20:39
-
 par salvinette » 12 Jan 2011, 21:00
par salvinette » 12 Jan 2011, 21:00
Je ne sais pas comment faire car j'ai tout juste débuter ma leçon et je viens de BAC PRO c'est dure pour moi !!!*
Je sais primitiver cos X et Sin X mais là il sont au carré donc je ne sais pas ... Que dois-je faire ????
-
salvinette
- Messages: 7
- Enregistré le: 12 Jan 2011, 20:39
-
 par salvinette » 12 Jan 2011, 21:12
par salvinette » 12 Jan 2011, 21:12
non pas du tout !!! pourquoi cela et d'aprés quoi ???
-
salvinette
- Messages: 7
- Enregistré le: 12 Jan 2011, 20:39
-
 par salvinette » 12 Jan 2011, 21:17
par salvinette » 12 Jan 2011, 21:17
Oké pour la 1°) j'ai trouver py/3 d'aprés ce que vous m'avais dit
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 12 Jan 2011, 21:26
par Arnaud-29-31 » 12 Jan 2011, 21:26

, ca vient du théorème de Pythagore vu en 4ème/3éme.
En effet, dans un triangle rectangle,
 = \frac{adjacent}{hypotenuse})
,
 = \frac{oppose}{hypotenuse})
donc

Or lé théorème de Pythagore nous dit que

Ensuite on utilise la propriété
.dx + \int_a^b g(x).dx = \int_a^b \left( f(x)+g(x) \right).dx)
.
Pour la question 2) je suppose que tu voulais écrire "Montrer que

"
Si tu intègre A par parties, ca donne quoi ?
-
salvinette
- Messages: 7
- Enregistré le: 12 Jan 2011, 20:39
-
 par salvinette » 12 Jan 2011, 21:52
par salvinette » 12 Jan 2011, 21:52
bien j'ai Sin x
-
salvinette
- Messages: 7
- Enregistré le: 12 Jan 2011, 20:39
-
 par salvinette » 12 Jan 2011, 22:00
par salvinette » 12 Jan 2011, 22:00
J'ai A= [(cos x) (sin x)] - intégrale (-sin x) (sin x) dx
-
salvinette
- Messages: 7
- Enregistré le: 12 Jan 2011, 20:39
-
 par salvinette » 12 Jan 2011, 22:06
par salvinette » 12 Jan 2011, 22:06
c'est quoi la primitif de (-sin x) (sin x) ???
-
Vahngal
- Membre Relatif
- Messages: 117
- Enregistré le: 28 Nov 2010, 15:33
-
 par Vahngal » 13 Jan 2011, 01:14
par Vahngal » 13 Jan 2011, 01:14
salvinette a écrit:c'est quoi la primitif de (-sin x) (sin x) ???
Il ne faut pas intégrer...
intégrale (-sin x) (sin x) dx = - intégrale ( sinx ) (sinx) dx = - intégrale (sinx)² dx = ?
N'oublie pas que l'on cherche A-B.
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 13 Jan 2011, 16:43
par Arnaud-29-31 » 13 Jan 2011, 16:43
Si on n'oublie pas les bornes, on a bien grâce à une intégration par parties

= ... ?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 43 invités
