Etude de fonctions
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
putny57
- Membre Naturel
- Messages: 85
- Enregistré le: 29 Déc 2005, 14:43
-
 par putny57 » 05 Mai 2006, 13:59
par putny57 » 05 Mai 2006, 13:59
Bonjour!J'aurai besoin d'aide pour une quetion que je n'arrive pas à résoudre!
On a une fonction =(x^3+6x^2+7x+6)/2*(x^2+1)) De dérivée
De dérivée:
=(x^4-4x^2+7)/2*(x^2+1)^2) Il faut prouver que pour tout x appartient à [0;+infini] que l'on a:
Il faut prouver que pour tout x appartient à [0;+infini] que l'on a: Et déduire que f'(x)>0 pour tout x réel.
Et déduire que f'(x)>0 pour tout x réel.Si quelqu'un peut m'aider,il sera bienvenu!
Merci beaucoup!
-
Zebulon
- Membre Complexe
- Messages: 2413
- Enregistré le: 01 Sep 2005, 10:06
-
 par Zebulon » 05 Mai 2006, 14:04
par Zebulon » 05 Mai 2006, 14:04
Bonjour,
calculez le discrimant de cette inéquation. On a alors

si et seulement si
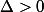
.
-
putny57
- Membre Naturel
- Messages: 85
- Enregistré le: 29 Déc 2005, 14:43
-
 par putny57 » 05 Mai 2006, 14:14
par putny57 » 05 Mai 2006, 14:14
Zebulon a écrit:calculez le discrimant de cette inéquation.
Comment ça le discriminant?Tu peux m'expliquer?Merci!!
-
yvelines78
- Membre Légendaire
- Messages: 6903
- Enregistré le: 15 Fév 2006, 21:14
-
 par yvelines78 » 05 Mai 2006, 14:24
par yvelines78 » 05 Mai 2006, 14:24
bonjour,
le delta est négatif
delta=b²-4ac=(-4)²-4*(1)*7=16-28
le polynôme n'a pas de racine et il du signe de a pour tout x
-
putny57
- Membre Naturel
- Messages: 85
- Enregistré le: 29 Déc 2005, 14:43
-
 par putny57 » 06 Mai 2006, 09:40
par putny57 » 06 Mai 2006, 09:40
C'est bon j'ai compris!
Mais comment on fait pour prouver que f'(x)>0 pour tout x réel.
On refait la même chose?
Merci!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 65 invités