Barycentres 3 points

[Number2]

Bonjour ! .. Je m'adresse à nouveau à vous .. Il y a ENCORE (--') une question qui me bloque !

A,B et C non alignés. D barycentre de (A;5) , (B;-2) et (C;-1)

1.faire une figure et placer D
la figure est faite, et je trouve AD=-AB-(1/2)BC

2. Ecrire A comme barycentre de B, C et D
Comment m'y prendre ?

3. Ecriré B comme barycentre de A, C et D
Si j'ai une démarche pour la 2., je pense que je pourrais faire cette question tout seul (quoi que... )

MERCI !

[Ben314]

Salut,
Pour montrer que A est barycentre de B,C,D affecté de certaint coefficients, il faut que tu rerouve une relation de la forme où la somme des trois ? est non nulle.
Pour ce faire, tu part d'une relation vectorielle contenant les points A,B,C et D (donc de celle que tu as trouvé au 1)) et tu introduit le point A partout où il n'est pas déjà présent.
Par exemple, tu écrit que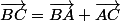

[Number2]

Salut,
Pour montrer que A est barycentre de B,C,D affecté de certaint coefficients, il faut que tu rerouve une relation de la forme où la somme des trois ? est non nulle.
Pour ce faire, tu part d'une relation vectorielle contenant les points A,B,C et D (donc de celle que tu as trouvé au 1)) et tu introduit le point A partout où il n'est pas déjà présent.
Par exemple, tu écrit que

La dernière étape du 1) était : AD = -AB -1/2AC
Alors en faisant ce que vous me dites j'obtiens : AD+AB+1/2AC=0
La somme est non nulle. Et donc ça suffit ?