bonjour,je bloque sur cet exercice.Si quelqu'un peut m'aider se serait sympa.merci par avance
EXCERCICE:
O,A et B sont 3 points non alignés du plan. On rapporte le plan au repère (O; OA;OB>).
Pour tout réel m non nul ,Gm désigne le barycentre des points pondérés (O; m - 2), (A; 2) et (B;m)
1) Construire G1 et G2
2) déterminer les coordonnées de Gm
3)a)Soit I le milieu de [OB]. Montrer que les vecteurs IGm et OA sont colinéaires
b)Déterminer l'ensemble des points Gm lorsque m décrit R*
c) Déterminer l'ensemble des points Gm lorsque m décrit [1; + l'infinie[
pour la premiere question j'ai trouvé:
pour G1:
OG1=OA + 1/2 OB (OG OA et OB sont des vecteurs)
pour G2:
OG2=2/4OA + 2/4 OB (OG OA OB sont des vecteurs)
cela est-il correct???
Pourriez vous m'aider pour les autres questions svp
Barycentre
10 messages
- Page 1 sur 1
Ce que tu dis ( et
et  ) est correct.
) est correct.
Pour la suite, comme on a colinéaire à
colinéaire à 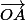 , l'ensemble des points
, l'ensemble des points 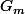 quand m parcourt
quand m parcourt 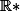 est la droite parallèle à (OA) et passant par I. Attention! On doit retirer I! En effet, si pour un certain m,
est la droite parallèle à (OA) et passant par I. Attention! On doit retirer I! En effet, si pour un certain m, 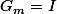 , alors
, alors  .
.
Donc finalement, l'ensemble des points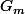 quand m parcourt
quand m parcourt 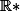 est la droite parallèle à (OA), passant par I, et privée de I.
est la droite parallèle à (OA), passant par I, et privée de I.
Je te laisse faire la c.
Bon courage.
Pour la suite, comme on a
Donc finalement, l'ensemble des points
Je te laisse faire la c.
Bon courage.
amber a écrit:pour la 3a)je pensé avoir compris ton raisonnement mais en faite ce n'est pas le cas.Pourrez tu m'expliquer stp.
Que n'as-tu pas compris? C'est seulement un calcul. Y a-t-il des étapes que tu ne comprends pas?
amber a écrit:et pour la 3b)comment fait on pour tracer une droite privée d'un point mais passant par ce point
merci par avance
On trace le droite et une petite croix sur le point ou alors ---[]---.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 143 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
