Réduire la longueur d'un vecteur
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
maxs15
- Messages: 5
- Enregistré le: 13 Nov 2010, 19:20
-
 par maxs15 » 13 Nov 2010, 19:27
par maxs15 » 13 Nov 2010, 19:27
Bonjour,
Je suis dans une impasse, en effet j'aurais besoin de réduire la longueur d'un vecteur.
Je sais que
- Code: Tout sélectionner
Longueur = sqrt(x^2 + y^2)
Mais je ne voit pas comment récupéré les coordonnée si je veux que longueur sois égale a 2 par exemple.
Merci de votre aide,
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 13 Nov 2010, 19:31
par Arnaud-29-31 » 13 Nov 2010, 19:31
Bonjour,
J'ai peur de ne pas tout avoir compris ...
On parle du vecteur
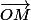
avec O l'origine d'un repère et (x,y) les coordonnées de M c'est ça ?
Et tu veux trouver un point N tel que
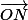
soit colinéaire au vecteur de départ mais d'une longueur précise (ici 2 dans ton exemple) ??
-
maxs15
- Messages: 5
- Enregistré le: 13 Nov 2010, 19:20
-
 par maxs15 » 13 Nov 2010, 20:36
par maxs15 » 13 Nov 2010, 20:36
Oui voila c'est sa
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 14 Nov 2010, 00:24
par Arnaud-29-31 » 14 Nov 2010, 00:24
Et bien si l'on a M(x,y), on peut poser
)
et dans ce cas
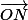
est colinéaire à
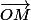
et

Si tu veux un vecteur
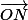
de longueur L, tu prendras
)
comme coordonnées pour N.
J'espère que ça répond à ta question ...
-
maxs15
- Messages: 5
- Enregistré le: 13 Nov 2010, 19:20
-
 par maxs15 » 14 Nov 2010, 19:53
par maxs15 » 14 Nov 2010, 19:53
Merci de votre aide c'est exactectement ce que je cherchais ;)
Et si le vecteur n'est pas de centre O, il me suffit seulement d'effectuer une translation aprés cela c'est bien sa?
-
maxs15
- Messages: 5
- Enregistré le: 13 Nov 2010, 19:20
-
 par maxs15 » 14 Nov 2010, 20:07
par maxs15 » 14 Nov 2010, 20:07
Voila un shema, si ce n'est pas de centre O, mais de A

Merci pour votre aide en tout cas, c'est sympa!
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 14 Nov 2010, 22:18
par Arnaud-29-31 » 14 Nov 2010, 22:18
C'est pareil sauf que
)
Tu prendras
}{sqrt{(x-x_A)^2+(y-y_A)^2}},\frac{L.(y-y_A)}{sqrt{(x-x_A)^2+(y-y_A)^2}}))
-
maxs15
- Messages: 5
- Enregistré le: 13 Nov 2010, 19:20
-
 par maxs15 » 16 Nov 2010, 21:23
par maxs15 » 16 Nov 2010, 21:23
Merci, c'est exactement ce que j'avais besoin, sa marche!
Merci de votre aide :we:
-
Arnaud-29-31
- Membre Complexe
- Messages: 2110
- Enregistré le: 06 Avr 2010, 15:00
-
 par Arnaud-29-31 » 16 Nov 2010, 21:41
par Arnaud-29-31 » 16 Nov 2010, 21:41
De rien !!!
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 155 invités

