DM Algèbre, pgcd.
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Maeva 05
- Messages: 3
- Enregistré le: 03 Nov 2010, 15:57
-
 par Maeva 05 » 03 Nov 2010, 16:09
par Maeva 05 » 03 Nov 2010, 16:09
Bonjour à tous :)
J'ai un DM d'algèbre à rendre pour vendredi, le problème est que je n'y comprends pas vraiment grand chose.. Et ça m'avancerait beaucoup si quelqu'un pouvait au moins me donner une piste pour la première question..
(Pour simplifier l'écriture du message, je mettrais X=alpha et Y=bêta).
Soit a et b des entiers.On note d=pgcd(a,b) et on introduit X, Y appartenant à Z tels que a=dX et b=dY. Le but de l'exercice est de calculer pgcd(a^3-b^3, (a-b)^3).
1. Montrer que a-b divise a^3-b^3.
2. Montrer que pgcd(a^3-b^3, (a-b)^3) = (a-b)d²pgcd(X²+XY+Y²,(X-Y)²)
3.a) Prouver que pgcd(X-Y, XY)=1
b) En déduire que pgcd(X²+XY+Y²,(X-Y)²) appartient à {1 , 3}, puis donner la condition sur X,Y permettant de séparer les deux cas.
4. Conclure.
Voilà..
Je vous remercie d'avance de vos éventuelles réponses..
Maeva :we:
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Nov 2010, 16:19
par Nightmare » 03 Nov 2010, 16:19
Salut,
1.
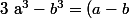(a^{2}+ab+b^{2}))
2. Poser comme dans les hypothèses a=dX et b=dY et remarquer aussi que a^3-b^3 et (a-b)^3 sont tous les deux divisibles par (a-b)
3.a) Identité de Bezout, sachant quand même que X et Y sont premiers entre eux !
Je te laisse réfléchir par toi même à la suite.
-
Maeva 05
- Messages: 3
- Enregistré le: 03 Nov 2010, 15:57
-
 par Maeva 05 » 03 Nov 2010, 16:47
par Maeva 05 » 03 Nov 2010, 16:47
Merci de ton aide, je comprends mieux ce qui est demandé maintenant.
Par contre à la question 2, je n'arrive toujours pas à montrer l'égalité, et je ne sais pas comment me servir de "a^3-b^3 et (a-b)^3 sont tous les deux divisibles par (a-b)" ..
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Nov 2010, 16:53
par Nightmare » 03 Nov 2010, 16:53
Reviens à la définition du PGCD : c'est le plus grand diviseur commun. Et il faut voir aussi une chose, c'est qu'un diviseur commun divise forcément le PGCD !
-
Maeva 05
- Messages: 3
- Enregistré le: 03 Nov 2010, 15:57
-
 par Maeva 05 » 03 Nov 2010, 17:38
par Maeva 05 » 03 Nov 2010, 17:38
Ca va faire plus d'une heure que j'essaie de comprendre, mais je n'y arrive absolument pas..
-
Nightmare
- Membre Légendaire
- Messages: 13817
- Enregistré le: 19 Juil 2005, 17:30
-
 par Nightmare » 03 Nov 2010, 18:13
par Nightmare » 03 Nov 2010, 18:13
Ce n'est pourtant vraiment pas compliqué .
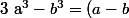(a^2+ab+b^2))
et
^3=(a-b)(a-b)^2)
Donc déjà, cela permet de dire que
^3)=(a-b)PGCD(a^{2}+ab+b^{2};(a-b)^{2}))
Ensuite en posant
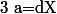
et
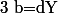
, on a que
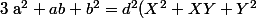)
et
^{2}=d^{2}(X-Y)^2)
donc d (=PGCD(a,b) ) est un diviseur commun de a²+ab+b² et (a-b)² ce qui permet d'écrire encore une fois que
^{2})=d^{2}PGCD(X^{2}+XY+Y^{2};(X-Y)^{2}))
On a donc bien
^{3})=(a-b)d^{2}PGCD(X^{2}+XY+Y^{2};(X-Y)^{2}))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 117 invités
