Equation
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
leszeus
- Membre Naturel
- Messages: 23
- Enregistré le: 23 Oct 2010, 14:05
-
 par leszeus » 23 Oct 2010, 14:48
par leszeus » 23 Oct 2010, 14:48
Bonjour !
Je bloque sur un exercice, ce serait sympa de m'aider :)
Voici l'énoncé :
Résoudre dans R l'équation :
x² + (m+1)x + m² = 0 ou m est un paramètre réel.
On distinguera plusieurs cas selon les valeurs de m.
Mes solutions :
m = 1 m = -1
x² + 2x + 1 = 0 x² + 1 = 0
(x + 1)² = 0 x² = -1
x = -racine de 1
donc x + 1 = -1
S = (-1) S = (-racine de 1)
-
uztop
- Membre Complexe
- Messages: 2396
- Enregistré le: 12 Sep 2007, 11:00
-
 par uztop » 23 Oct 2010, 15:00
par uztop » 23 Oct 2010, 15:00
Salut,
x²=-1 n'a pas de solution vu qu'un carré est toujours positif.
Mais, pour résoudre ton problème, il faut raisonner de façon plus générale. Est ce que tu as appris ce qu'est un discriminant? Est ce que tu peux calculer le discriminant (en fonction de m) pour ton équation?
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 23 Oct 2010, 15:02
par Jimm15 » 23 Oct 2010, 15:02
Bonjour,
Il faut commencer par calculer le discriminant du trinôme
x+m^2)
. Il dépendra donc de

.
-
leszeus
- Membre Naturel
- Messages: 23
- Enregistré le: 23 Oct 2010, 14:05
-
 par leszeus » 23 Oct 2010, 15:09
par leszeus » 23 Oct 2010, 15:09
le discriminant, ca me dit quelque chose, on a fait le cour juste avant les vacances, en mode tres rapide... et avec la grêve on a rater pas mal de choses...
J'ai appris delta ca je suis sur.
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 23 Oct 2010, 15:16
par Jimm15 » 23 Oct 2010, 15:16
Un trinôme du second degré est un polynôme dexpression
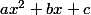
avec
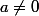
.
Pour résoudre
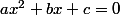
, on doit utiliser ce quon appelle le discriminant

du trinôme. Il vaut
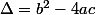
.
Remarque : Si

ou

est nul, il nest alors pas nécessaire dutiliser le discriminant.
Si 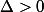
, léquation
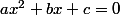
admet deux solutions distinctes :
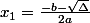
et

.
Si 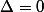
, léquation
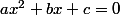
admet une unique solution :
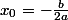
.
Si 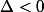
, léquation
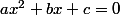
nadmet aucune solution.
Dautre part, le signe de

renseigne sur le signe de
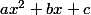
.
 Daprès Guide ABC Mathématiques 1re S Nathan, 2009.
Daprès Guide ABC Mathématiques 1re S Nathan, 2009.
-
leszeus
- Membre Naturel
- Messages: 23
- Enregistré le: 23 Oct 2010, 14:05
-
 par leszeus » 23 Oct 2010, 15:48
par leszeus » 23 Oct 2010, 15:48
Merci Jimm !!
Je vais lire et reflechir à tout ça et je vais reposter mes réponses dans quelques heures.
-
leszeus
- Membre Naturel
- Messages: 23
- Enregistré le: 23 Oct 2010, 14:05
-
 par leszeus » 23 Oct 2010, 16:56
par leszeus » 23 Oct 2010, 16:56
Je suis bloqué...
x2 + (m + 1) + m2 = 0
delta = b2 - 4ac
a = 1, b = m + 1, c = m2
donc delta = (m+1) au carré - 4m2
delta = ( m+1 - 4m2 ) ( m+1 + 4m2 )
Apres c'est censé me mener à ou ? :mur:
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 23 Oct 2010, 17:03
par Jimm15 » 23 Oct 2010, 17:03
Tu peux développer lexpression de

.
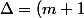^2-4m^2=m^2+2m+1-4m^2=-3m^2+2m+1)
.
Donc le signe de

dépend de

et les solutions de
x+m^2=0)
dépendent du signe de

.
Vois-tu ce quil va falloir faire ?
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 23 Oct 2010, 17:09
par Rebelle_ » 23 Oct 2010, 17:09
Bonjour =)
Je pense que l'on peut remarquer que l'expression du discriminant admet une factorisation triviale qui permet d'en déduire facilement le signe, non ? :)
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 23 Oct 2010, 17:12
par Jimm15 » 23 Oct 2010, 17:12
Rebelle_ a écrit:Bonjour =)
Je pense que l'on peut remarquer que l'expression du discriminant admet une factorisation triviale qui permet d'en déduire facilement le signe, non ?

Bien vu.
Je te laisse la trouver
leszeus.
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 23 Oct 2010, 17:14
par Rebelle_ » 23 Oct 2010, 17:14
Désolée, c'était pour mettre en lumière le fait qu'il ne faille pas nécessairement développer :)
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 23 Oct 2010, 17:16
par Jimm15 » 23 Oct 2010, 17:16
Rebelle_ a écrit:Désolée, c'était pour mettre en lumière le fait qu'il ne faille pas nécessairement développer

Oui, et cest une très bonne intervention. Merci.
-
leszeus
- Membre Naturel
- Messages: 23
- Enregistré le: 23 Oct 2010, 14:05
-
 par leszeus » 23 Oct 2010, 17:57
par leszeus » 23 Oct 2010, 17:57
Jimm15 a écrit:Tu peux développer lexpression de

.
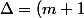^2-4m^2=m^2+2m+1-4m^2=-3m^2+2m+1)
.
Donc le signe de

dépend de

et les solutions de
x+m^2=0)
dépendent du signe de

.
Vois-tu ce quil va falloir faire ?
Si le signe de

dépend de

alors si
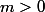
alors
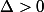
donc il y aura deux racines.
Si

alors
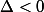
donc il y aura une racine.
Ayé, j'ai trouvé ?

-
leszeus
- Membre Naturel
- Messages: 23
- Enregistré le: 23 Oct 2010, 14:05
-
 par leszeus » 23 Oct 2010, 17:57
par leszeus » 23 Oct 2010, 17:57
Pour la factorisation triviale, je ne sais pas ce que c'est donc...
Sorry pour le double post j'ai pas fait exprêt :--:
-
Rebelle_
- Membre Irrationnel
- Messages: 1383
- Enregistré le: 27 Aoû 2010, 18:04
-
 par Rebelle_ » 23 Oct 2010, 18:01
par Rebelle_ » 23 Oct 2010, 18:01
leszeus a écrit:Pour la factorisation triviale, je ne sais pas ce que c'est donc...
La factorisation vient de l'identité remarquable bien connue : a² - b² = (a+b)(a-b). Ici quelles sont les valeurs de a et b ?
Je laisse la suite à Jimm15 qui avait commencé =)
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 23 Oct 2010, 18:07
par Jimm15 » 23 Oct 2010, 18:07
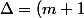^2-4m^2=(m+1)^2-(2m)^2)
.
Oups, jen ai trop dit ! :we:
-
leszeus
- Membre Naturel
- Messages: 23
- Enregistré le: 23 Oct 2010, 14:05
-
 par leszeus » 23 Oct 2010, 18:08
par leszeus » 23 Oct 2010, 18:08
Rebelle_ a écrit:La factorisation vient de l'identité remarquable bien connue : a² - b² = (a+b)(a-b). Ici quelles sont les valeurs de a et b ?
Je laisse la suite à Jimm15 qui avait commencé =)
Ah bah ça je l'avais déjà proposé

donc delta = (m+1)² - 4m²
delta = (m+1 - 4m²) (m+1 + 4m²)
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 23 Oct 2010, 18:09
par Jimm15 » 23 Oct 2010, 18:09
Sauf que tu as écrit
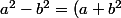(a-b^2))
ce qui est faux...
-
leszeus
- Membre Naturel
- Messages: 23
- Enregistré le: 23 Oct 2010, 14:05
-
 par leszeus » 23 Oct 2010, 18:14
par leszeus » 23 Oct 2010, 18:14
je corrige,
Delta = (m+1 - 2m) (m+1 + 2m)
J'ai vraiment du mal dis donc :(
-
Jimm15
- Membre Rationnel
- Messages: 734
- Enregistré le: 16 Déc 2006, 20:44
-
 par Jimm15 » 23 Oct 2010, 18:14
par Jimm15 » 23 Oct 2010, 18:14
Tu réduis ce qui est dans les parenthèses et tu en déduis les solutions de
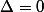
.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités
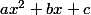 avec
avec 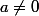 .
.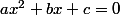 , on doit utiliser ce quon appelle le discriminant
, on doit utiliser ce quon appelle le discriminant  du trinôme. Il vaut
du trinôme. Il vaut 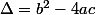 .
. ou
ou  est nul, il nest alors pas nécessaire dutiliser le discriminant.
est nul, il nest alors pas nécessaire dutiliser le discriminant.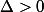 , léquation
, léquation 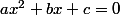 admet deux solutions distinctes :
admet deux solutions distinctes :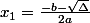 et
et  .
.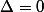 , léquation
, léquation 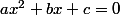 admet une unique solution :
admet une unique solution :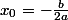 .
.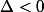 , léquation
, léquation 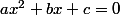 nadmet aucune solution.
nadmet aucune solution. renseigne sur le signe de
renseigne sur le signe de 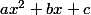 .
.

