Produit
5 messages
- Page 1 sur 1
produit
Bonjour, je recherche (produit de k=n+2 à 2n+3 de k) >ou égal au (produit de k=0 à n+1 de (n+2)!), pouvais vous m'aidez svp
En retirant la factorielle après le (n+2) de ton premier post, tout de suite ça passe mieux... Enfin l'idéal c'est de poster l'exercice complet, nul n'est pas à l'abri d'une erreur dans le raisonnement...
Bon si j'ai bien deviné ton raisonnement tu es arrivée à montrer, partant de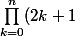! \ge (n+1)!^{n+1}) , que
, que 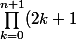! \ge (2n+3)!(n+1)!^{n+1} = (n+1)!^{n+2}\prod_{k=n+2}^{2n+3}k) . Et tu aimerais donc montrer que
. Et tu aimerais donc montrer que 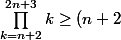^{n+2}) .
.
Combien y a-t-il de termes dans le produit de gauche ?
Bon si j'ai bien deviné ton raisonnement tu es arrivée à montrer, partant de
Combien y a-t-il de termes dans le produit de gauche ?
5 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 83 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
