DM math spé Arithmétique
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Galdius
- Messages: 2
- Enregistré le: 02 Oct 2010, 15:20
-
 par Galdius » 02 Oct 2010, 15:39
par Galdius » 02 Oct 2010, 15:39
<br />1)sachant que n \in \mathbb{Z} démontrez que n^2+3n+2 est divisible par n+2<br />(pour sa j'ai factoriser je tombe sur n+2|(n+2)-n-2 jpense pas que c'est bon ^^)<br />2) soit 3n^2+13n+23 =(n+2)(3n+7)+9 determiner les entiers relatifs n pour lesquels 3n^2+13n+23 est divisible par n+2<br />3) soit C la courbe y = \frac{3n^2+13n+23}{n^2+3n+2} dans le plain muni d'n repere (O;i;j). Y a t'il des point de C dont les coordonnées sont des entiers ?)
Merci d'avance de votre aide
Edit :jdoi mettre ou les TEX? parce que sa a pas marcher '-'

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 02 Oct 2010, 15:52
par Olympus » 02 Oct 2010, 15:52
Salut !
Pour la première, il te suffira de voir que
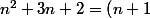 \left( n+2 \right))
.
Pour la deuxième, tout d'abord t'as

( sinon on ne peut pas parler de divisibilité ) .

est divisible par

, donc

.

.

.
Je crois que tu peux continuer maintenant .
Pour la 3)
Tu peux voir par toi-même en simplifiant ta fraction .
-
Galdius
- Messages: 2
- Enregistré le: 02 Oct 2010, 15:20
-
 par Galdius » 02 Oct 2010, 16:55
par Galdius » 02 Oct 2010, 16:55
merci mais Je crois que je peux pas utilisé cette réponce :'( Le prof nous a indiqué et insisté que l'on doit oublier La division et qu'en arithmétique c'est sur la forme a| b ( les fraction sont donc interdites :/

-
Olympus
- Membre Irrationnel
- Messages: 1668
- Enregistré le: 12 Mai 2009, 11:00
-
 par Olympus » 02 Oct 2010, 17:12
par Olympus » 02 Oct 2010, 17:12
Ton prof doit être assez... spécial dit donc... Je comprendrai qu'il interdise cela temporairement pour que vous vous habituez à utiliser l'autre forme, mais pas qu'il l'interdise sous prétexte que c'est anti-arithmétique .
Donc pour la deuxième :

\left(3n+7\right) + 9 \right.)

.
( qu'un changement de notation, cela revient au même )
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 70 invités