Question complexe
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Reynolds
- Membre Naturel
- Messages: 23
- Enregistré le: 27 Juin 2010, 15:16
-
 par Reynolds » 12 Sep 2010, 19:24
par Reynolds » 12 Sep 2010, 19:24
Bonjour j'aurais deux question a vous poser:
1) Soit f une homographie de forme
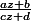
et ad-bd diffèrent de 0, montrer que f est bijective
Alors j'ai montré facilement l'injectivité mais je ne trouve pas pour la surjectivité, je prend un f dans l'ensemble d'arrivé mais je ne vois pas quoi en faire, j'ai essayé par l'absurde mais je n'y arrive pas.
2) Pouvez vous m'aider a simplifier cette expression:

Merci d'avance
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 12 Sep 2010, 19:50
par girdav » 12 Sep 2010, 19:50
Bonjour,
pour le 1 tu peux résoudre en

l'équation

. D'ailleurs, je pense qu'il faut préciser les ensembles de départ et d'arrivée.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 12 Sep 2010, 19:55
par girdav » 12 Sep 2010, 19:55
Pour le 2, on a
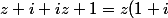+(1+i))
et
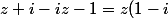-(1-i))
.
-
Reynolds
- Membre Naturel
- Messages: 23
- Enregistré le: 27 Juin 2010, 15:16
-
 par Reynolds » 12 Sep 2010, 20:39
par Reynolds » 12 Sep 2010, 20:39
C'est a dire,
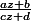
=Z?
Les ensembles sont C\ d/c

C\ a/c
et merci pour la simplification
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 12 Sep 2010, 20:41
par girdav » 12 Sep 2010, 20:41
Oui, pour

on résout en

l'équation que tu viens d'écrire : on ne fait que rechercher un antécédent.
-
Reynolds
- Membre Naturel
- Messages: 23
- Enregistré le: 27 Juin 2010, 15:16
-
 par Reynolds » 13 Sep 2010, 19:00
par Reynolds » 13 Sep 2010, 19:00
Ok, suite a ma journée de cours j'ai essayé d'exploiter ton idée, donc j'ai fait:
Z appartient a C\ a/c
j'ai posé l'équation et j'en suis arrivé à
z=

Donc si je peux conclure que z appartient a C\ -d/c c'est gagné?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 13 Sep 2010, 19:12
par girdav » 13 Sep 2010, 19:12
Voilà, pour le montrer on calcule

et on devrait voir que c'est non nul.
-
Reynolds
- Membre Naturel
- Messages: 23
- Enregistré le: 27 Juin 2010, 15:16
-
 par Reynolds » 13 Sep 2010, 19:17
par Reynolds » 13 Sep 2010, 19:17
Oulah j'ai jamais fait additionner un élement et un ensemble, pourrais je avoir plus d'indications?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 13 Sep 2010, 20:16
par girdav » 13 Sep 2010, 20:16
Il n'est pas question de ça : je voulais juste vérifier que le

obtenue est différent de

.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
