Forme générale d'endomorphismes

par **Wolowitz** » 12 Sep 2010, 21:40

Finalement, a-t-on la matrice suivante?

par **girdav** » 12 Sep 2010, 21:43

Normalement oui, mais il faut préciser une condition sur

,

et

pour que les deux premiers vecteurs colonne soient linéairement indépendants.

par **Wolowitz** » 12 Sep 2010, 21:51

je crois que c'est

par **Wolowitz** » 12 Sep 2010, 22:06

je crois que c'est

par **Wolowitz** » 13 Sep 2010, 15:36

Bonjour,

Bon j'ai donc la matrice

ai-je donc donc terminé l'exercice?

l'énoncé demandant de trouver la forme générale des endomorphisme vérifiant

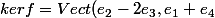Imf={(x,y,z,t);x+2y-3z=0 et x+t=0}

Merci

par **Doraki** » 13 Sep 2010, 15:44

Il faut rajouter la condition ad <> bc.

Si ad = bc ça fait que f(e1) et f(e2) sont colinéaires, et donc Im f est trop petit et Ker f est trop grand.

par **Doraki** » 13 Sep 2010, 15:47

Wolowitz a écrit:je crois que c'est

Comment tu fais pour passer de (3a-2b,b,a,-3a+2b) et (3c-2d,d,c,-3c+2d) non colinéaires à un truc aussi bizarre ?

Pour, au hasard, a=1,b=1,c=2,d=3, les deux vecteurs sont non colinéaires, et ça contredit tout ce que tu as dit.

par **Wolowitz** » 13 Sep 2010, 17:18

Je me disais que si

donc f(e1) est une combinaison linéaire de f(e2)

comme on veut que les vecteurs f(e1)et f(e2) soient indépendants je me suis dit que

puis on veut que

c'est pour cela que j'ai trouvé

Bon c'est faux, et j'aimerais bien votre aide pour trouver les conditions sur a, b, c et d pour que les deux premiers vecteurs colonnes soient linéairement indépendants.

par **girdav** » 13 Sep 2010, 17:36

On peut regarder la matrice formée des deux premières colonnes de la matrice que tu as écrite. Il faut que cette matrice soit de rang 2. Pour cela, on demande à ce que l'un des sous déterminants d'ordre 2 de cette matrice soit non nul. Mais en fait tous ces déterminants sont égaux à une constante multiplicative près (qui ne dépend heureusement ni de a,b,c ou d).

par **Wolowitz** » 13 Sep 2010, 17:49

Ah d'accord on a det1=(3a-2b)d-b(3c-2d)=3ad-3bc
det2= bc-ad
det3=a(-3c+2d) - c(-3a+2b)=2ad-2bc

det1=(3det3)/2
det2=-det3/2

l'énoncé dit de donner la forme générale de l'endomorphisme, donner sa matrice répond à la question?

par **girdav** » 13 Sep 2010, 17:58

Si on ajoute la condition sur les paramètres, oui.

par **Doraki** » 13 Sep 2010, 18:01

Wolowitz a écrit:c'est pour cela que j'ai trouvé
Bon c'est faux, et j'aimerais bien votre aide pour trouver les conditions sur a, b, c et d pour que les deux premiers vecteurs colonnes soient linéairement indépendants.

Si tu avais mis "ou" à la place de "et", ça aurait été bon.

par **Wolowitz** » 13 Sep 2010, 18:30

Ok merci à vous et bonne soirée

Forme générale d'endomorphismes

Qui est en ligne