Forme générale d'endomorphismes
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Wolowitz
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2010, 20:00
-
 par Wolowitz » 10 Sep 2010, 20:07
par Wolowitz » 10 Sep 2010, 20:07
Bonsoir,
cet exercice m'embête, et je suis complètement à la ramasse
Donner la forme générale des endomorphisme de

tels que
kerf=Vect(

)
Imf={(x,y,z,t);x+2y-3z=0 et x+t=0}
bon j'ai
 = 2f(e_3) et f(e_4)=-f(e_1))
et je bloque :hein:
Bonne soirée et merci.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 10 Sep 2010, 20:46
par girdav » 10 Sep 2010, 20:46
Bonjour,
si tu bloques, c'est sans doute parce que tu n'arrives pas à exploiter la condition sur l'image.
Tu peux commencer par chercher une base de l'image, disons

(elle est de dimension deux). Il faut que l'espace engendré par
,f(e_2),f(e_3),f(e_4)})
soit le même que l'espace engendré par

. Or
,f(e_2),f(e_3),f(e_4)\} =\mathrm{Vect}\{f(e_1),f(e_2)\})
, ce qui impose déjà quelque chose sur
)
et
)
.
-
Wolowitz
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2010, 20:00
-
 par Wolowitz » 10 Sep 2010, 21:17
par Wolowitz » 10 Sep 2010, 21:17
Il faut que l'espace engendré par
,f(e_2),f(e_3),f(e_4)})
soit le même que l'espace engendré par

.
=>Vect
,f(e_2),f(e_3),f(e_4)})
=Vect

=>Vect
,f(e_2)})

cela implique-t-il
=v_1 et f(e_2)=v_2)
?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 10 Sep 2010, 21:26
par girdav » 10 Sep 2010, 21:26
Malheureusement non, puisque en permutant
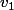
et
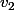
(ce qui ne change rien aux espaces engendrés) on pourrait déduire que v_1 =v_2, ce qui est moyen pour une base.
En revanche, on sait que
\in\mathrm{Vect}\{v_1,v_2\})
.
-
Wolowitz
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2010, 20:00
-
 par Wolowitz » 10 Sep 2010, 21:33
par Wolowitz » 10 Sep 2010, 21:33
f(e2) aussi appartient à Vect(v1,v2) nn?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 10 Sep 2010, 21:40
par girdav » 10 Sep 2010, 21:40
Wolowitz a écrit:f(e2) aussi appartient à Vect(v1,v2) nn?
Oui. Mais pourquoi ne pas essayer de voir qui sont
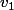
et
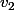
?
-
Wolowitz
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2010, 20:00
-
 par Wolowitz » 11 Sep 2010, 10:08
par Wolowitz » 11 Sep 2010, 10:08
bonjour
Je ne trouve toujours pas comment exprimer v1,et v2.
 \in Vect(v1,v2) => \forall (\lambda_1, \lambda_2) \in K^2 f(e1)=\lambda _1v1+ \lambda 2_ v2)
et puis je ne vois pas trop
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 11 Sep 2010, 10:12
par girdav » 11 Sep 2010, 10:12
Wolowitz a écrit:bonjour
Je ne trouve toujours pas comment exprimer v1,et v2.
 \in Vect(v1,v2) => \forall (\lambda_1, \lambda_2) \in K^2 f(e1)=\lambda _1v1+ \lambda 2_ v2)
et puis je ne vois pas trop
Il faut plutôt d'aider de ce que l'on sait sur l'image par l'énoncé.
-
Wolowitz
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2010, 20:00
-
 par Wolowitz » 11 Sep 2010, 18:30
par Wolowitz » 11 Sep 2010, 18:30
e1=
)
e1

Im f =>
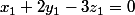
et

or
\in{Vect}\{v_1,v_2\})
et je suis bloqué. :hum:
Puis je n'arrive pas à relier les deux conditions.
-
Wolowitz
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2010, 20:00
-
 par Wolowitz » 12 Sep 2010, 10:06
par Wolowitz » 12 Sep 2010, 10:06
Bonjour
svp expliquez-moi juste comment on exploite la condition
Imf={(x,y,z,t);x+2y-3z=0 et x+t=0}
-
Purrace
- Membre Rationnel
- Messages: 536
- Enregistré le: 10 Déc 2006, 16:06
-
 par Purrace » 12 Sep 2010, 10:22
par Purrace » 12 Sep 2010, 10:22
tu peux donner le vectoriel qui engendre ton espace im(f) en deduire une base
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 12 Sep 2010, 10:23
par girdav » 12 Sep 2010, 10:23
Si

est dans l'image alors

et

donc
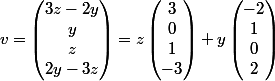
. Dès lors, tu dois être capable de trouver les vecteurs qui engendrent l'image.
-
Wolowitz
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2010, 20:00
-
 par Wolowitz » 12 Sep 2010, 10:56
par Wolowitz » 12 Sep 2010, 10:56
donc Imf=Vect((3,0,1,-3),(-2,1,0,2))
dim im f)=2
donc une base de Im f est(3,0,1,-3),(-2,1,0,2)?
-
Wolowitz
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2010, 20:00
-
 par Wolowitz » 12 Sep 2010, 11:36
par Wolowitz » 12 Sep 2010, 11:36
donc Imf=Vect((3,0,1,-3),(-2,1,0,2))
dim im f)=2
donc une base de Im f est(3,0,1,-3),(-2,1,0,2)?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 12 Sep 2010, 11:55
par girdav » 12 Sep 2010, 11:55
Si mes calculs sont corrects, oui.
-
Wolowitz
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2010, 20:00
-
 par Wolowitz » 12 Sep 2010, 14:01
par Wolowitz » 12 Sep 2010, 14:01
D'accord, et ainsi comment dois-je faire pour trouver la forme générale des endomorphisme vérifiant
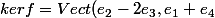)
Imf={(x,y,z,t);x+2y-3z=0 et x+t=0}
(je ne comprends pas trop le terme de forme générale)
-
Wolowitz
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2010, 20:00
-
 par Wolowitz » 12 Sep 2010, 14:52
par Wolowitz » 12 Sep 2010, 14:52
D'accord, et ainsi comment dois-je faire pour trouver la forme générale des endomorphisme vérifiant
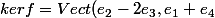)
Imf={(x,y,z,t);x+2y-3z=0 et x+t=0}
(je ne comprends pas trop le terme de forme générale)
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 12 Sep 2010, 14:52
par girdav » 12 Sep 2010, 14:52
L'espace vectoriel des endomorphismes de
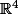
est
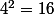
. Je ne sais pas si tu es familier avec la notion de matrice d'un endomorphisme, sinon tu peux voir ça comme un tableau
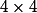
où les colonnes sont les vecteurs
)
,
)
,
)
,
)
.
Les conditions sur le noyau nous disent qu'il suffit de déterminer
)
et
)
.
-
Wolowitz
- Membre Naturel
- Messages: 20
- Enregistré le: 10 Sep 2010, 20:00
-
 par Wolowitz » 12 Sep 2010, 21:08
par Wolowitz » 12 Sep 2010, 21:08
Puis pour les lignes de la matrice j'aurai (e1,e2,e3,e4)?
(e1,e2,e3,e4) est ce la base canonique de l'endomorphisme?
 \in Vect((3,0,1,-3),(-2,1,0,2)))
mais que puis je déduire d'autre?
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 12 Sep 2010, 21:16
par girdav » 12 Sep 2010, 21:16
Donc il existe des constantes

et

telles que
 =a\begin{pmatrix}3\\0\\1\\-3\end{pmatrix}+b\begin{pmatrix}-2\\1\\0\\2\end{pmatrix})
et pareil pour
)
(avec des constantes

et

par exemple) de façon à ce que les deux vecteurs soient non nuls et non proportionnels.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 51 invités