Probleme d'intégrale
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
aurelie1584
- Membre Naturel
- Messages: 22
- Enregistré le: 08 Sep 2010, 18:37
-
 par aurelie1584 » 08 Sep 2010, 19:08
par aurelie1584 » 08 Sep 2010, 19:08
si cela inspire quelqu'un !! merci !
le but de cette question est de calculer une valeur approchée de I= intégrale de 1 à 2 de f(x)dx
avec f(x) =exp(x -1-xexp(x)
on ne cherche pas a effectuer un calcul direct
pour tout entier naturel k on pose Uk= intégrale de 1 à 2 de xexp(-kx)dx et pour tout entier naturel n Rn= intégrale de 1 à 2 de x(exp(-nx)/1-exp(-x))
montrer que pou tout entier naturel n, la somme (pour k=0 jusque n) de U(k+1) + R(n+2)= I
b) a l'aide d'une intégration par partie calculer pour tout entier naturel non nul k l'intégral Uk
c) montrer que pour tout entier naturel n 0
d) citer un entier naturel n pour lequel R(n+2)< 10^-3 obtenir une valeure approchée à 10^-3 pres et de la forme q.10^-3 ou q un entier.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 08 Sep 2010, 19:10
par girdav » 08 Sep 2010, 19:10
Bonjour,
pour la question a tu peux utiliser la somme d'une suite géométrique et le fait que l'intégral d'une somme est la somme des intégrales.
-
aurelie1584
- Membre Naturel
- Messages: 22
- Enregistré le: 08 Sep 2010, 18:37
-
 par aurelie1584 » 08 Sep 2010, 19:16
par aurelie1584 » 08 Sep 2010, 19:16
girdav a écrit:Bonjour,
pour la question a tu peux utiliser la somme d'une suite géométrique et le fait que l'intégral d'une somme est la somme des intégrales.
oui j'avais penser cela pour l'intégral du somme par contre je n'avais pas penser aux suites. Je ne vois pas trop encore mais je vais essayer.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 08 Sep 2010, 19:18
par girdav » 08 Sep 2010, 19:18
Calcule dans un premier temps pour

fixé
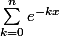
.
-
aurelie1584
- Membre Naturel
- Messages: 22
- Enregistré le: 08 Sep 2010, 18:37
-
 par aurelie1584 » 08 Sep 2010, 19:24
par aurelie1584 » 08 Sep 2010, 19:24
je suis désolée je ne suis vraiment pas douée ! je ne vois pas ! x fixé c'est a dire ?
-
aurelie1584
- Membre Naturel
- Messages: 22
- Enregistré le: 08 Sep 2010, 18:37
-
 par aurelie1584 » 08 Sep 2010, 19:27
par aurelie1584 » 08 Sep 2010, 19:27
parce que je commence a visualiser le truc mais je ne vois pas comment cette intégralke peut etre un suite. je n'ai jamais vu ca avec des exp encore moins avec une intégrale. je ne vois pas ou est la raison de la suite par exemple
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 08 Sep 2010, 19:28
par girdav » 08 Sep 2010, 19:28
En fait on veut d'abord simplifier l'expression de la fonction à intégrer. Ce que je veux dire, c'est calculer pour

quelconque la somme de mon message précédent.
-
aurelie1584
- Membre Naturel
- Messages: 22
- Enregistré le: 08 Sep 2010, 18:37
-
 par aurelie1584 » 08 Sep 2010, 19:35
par aurelie1584 » 08 Sep 2010, 19:35
mais pourquoi enlever le x qui est en facteur ? et je ne sais pas calculer une somme exponnentielle.
-
girdav
- Membre Complexe
- Messages: 2425
- Enregistré le: 21 Nov 2008, 21:22
-
 par girdav » 08 Sep 2010, 19:39
par girdav » 08 Sep 2010, 19:39
Oui, je suis bien conscient du fait que le

en facteur va intervenir, mais le gros du problème est de calculer la-dite somme. Que dirais-tu si on pose

?
-
aurelie1584
- Membre Naturel
- Messages: 22
- Enregistré le: 08 Sep 2010, 18:37
-
 par aurelie1584 » 08 Sep 2010, 19:41
par aurelie1584 » 08 Sep 2010, 19:41
que c'est une fonction positive décroissante qui tend vers 0
-
aurelie1584
- Membre Naturel
- Messages: 22
- Enregistré le: 08 Sep 2010, 18:37
-
 par aurelie1584 » 08 Sep 2010, 19:42
par aurelie1584 » 08 Sep 2010, 19:42
oups pardon j'ai lu g(x) oui ok je vois je fais le calcule et je vois ce que ca donne
-
aurelie1584
- Membre Naturel
- Messages: 22
- Enregistré le: 08 Sep 2010, 18:37
-
 par aurelie1584 » 08 Sep 2010, 19:53
par aurelie1584 » 08 Sep 2010, 19:53
ok je me suis pris la tete j'ai cherché trop compliqué donc la je pose q=exp(-x) pour avoir une suite Uk il faut que Uo=x comme ca j'ai Uk=Uoq^k
=xexp(-xk)
du coup la somme je trouve x + (1-exp(-kx-1))/1-exp(-x) et ca ressemble pas mal a Rn
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 61 invités
